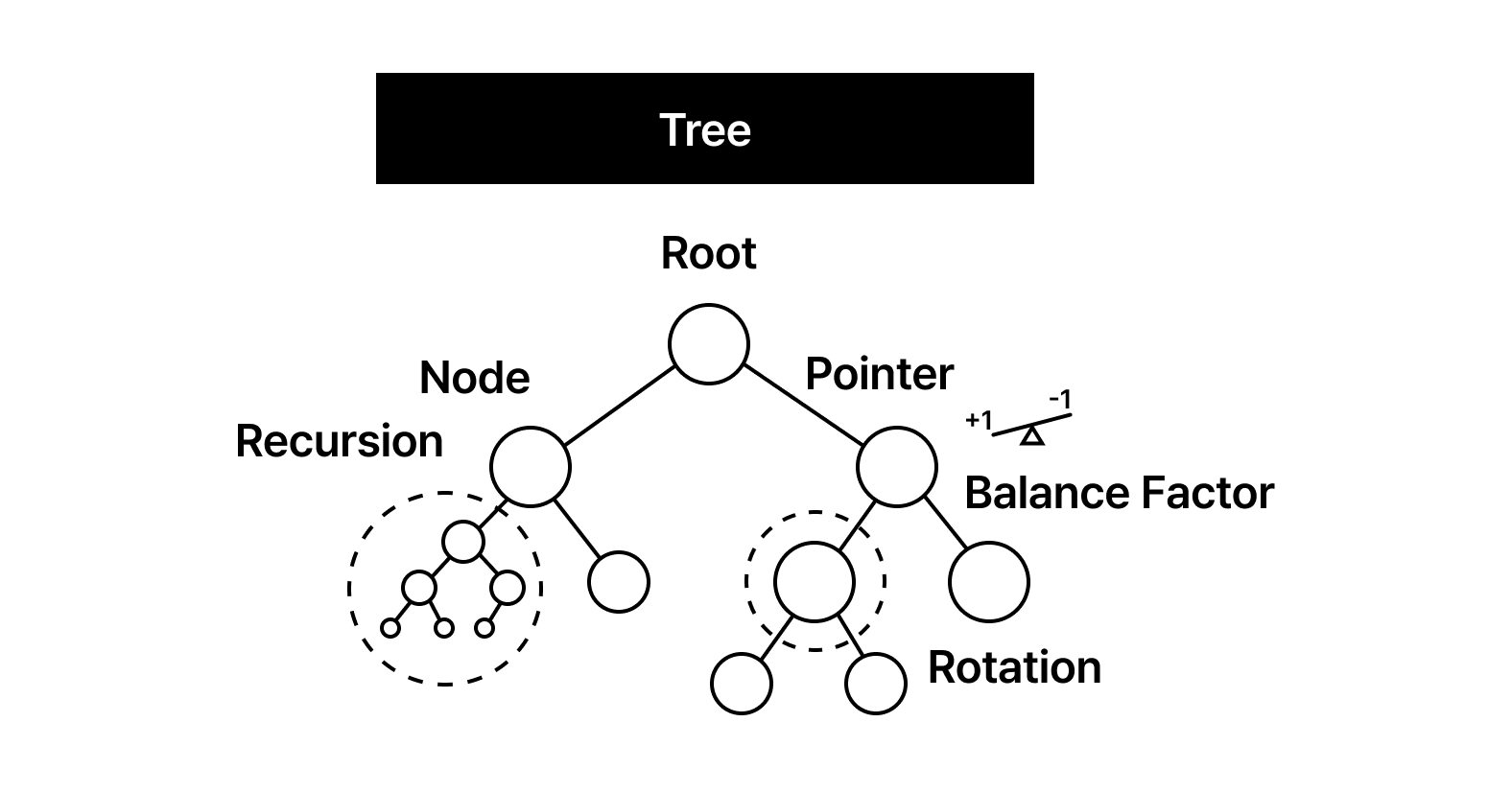
[Data Structure] Tree
우리는 흔히 데이터를 ‘쌓는다’고 표현하지만, 실제 엔지니어링의 세계에서 데이터는 단순히 적재되는 대상이 아닙니다. 데이터 사이의 관계가 선형적인 순서를 넘어 복잡한 위계를 형성하기 시작할 때, 배열이나 연결 리스트와 같은 1차원적 접근은 곧 치명적인 성능 병목에 봉착합니다. 수억 개의 데이터 속에서 단 몇 번의 연산만으로 원하는 정보를 찾아내야 하는 탐색의 문제, 혹은 파일 시스템이나 조직도처럼 본질적으로 계층적인 구조를 표현해야 하는 설계의 지점에서 우리는 ‘트리(Tree)’라는 해답을 마주하게 됩니다.
트리는 단순한 자료구조를 넘어 무질서한 엔트로피 상태의 데이터를 지능적인 신경망으로 변모시키는 아키텍처입니다. 효율적인 인덱싱은 곧 최단 경로를 찾아가는 논리적 흐름을 설계하는 일과 같습니다. 트리는 바로 그 흐름의 정점에 서 있습니다.
🧩 Tree
트리는 데이터 사이의 계층을 추상화한 그래프(Graph)의 특수한 부분 집합입니다. 하지만 단순히 ‘그래프의 일종’이라고 치부하기엔 트리가 가진 구조적 강제성이 엔지니어링에 주는 이득이 너무나 거대합니다. 트리의 핵심은 ‘비순환성(Acyclic)’과 ‘연결성(Connected)’의 결합에 있습니다. 임의의 두 노드를 잇는 경로가 단 하나뿐이라는 이 수학적 사실은, 데이터 탐색 시 결정해야 할 선택지를 기하급수적으로 줄여주는 필터 역할을 수행합니다.
컴퓨터 과학에서 트리는 $V$개의 정점(Vertex)과 $V-1$개의 간선(Edge)으로 이루어진 최소 연결 그래프로 정의됩니다. 여기서 간선 하나를 더하면 사이클(Cycle)이 발생하고, 하나를 제거하면 그래프는 분절됩니다. 이 위태로운 균형이 바로 트리가 데이터의 위계(Hierarchy)를 완벽하게 보존하는 비결입니다. 배열이 물리적 인접성을 이용해 $O(1)$의 접근성을 얻었다면, 트리는 이 계층적 위상을 이용해 $O(N)$의 선형 탐색 시간을 $O(\log N)$의 영역으로 끌어내립니다.
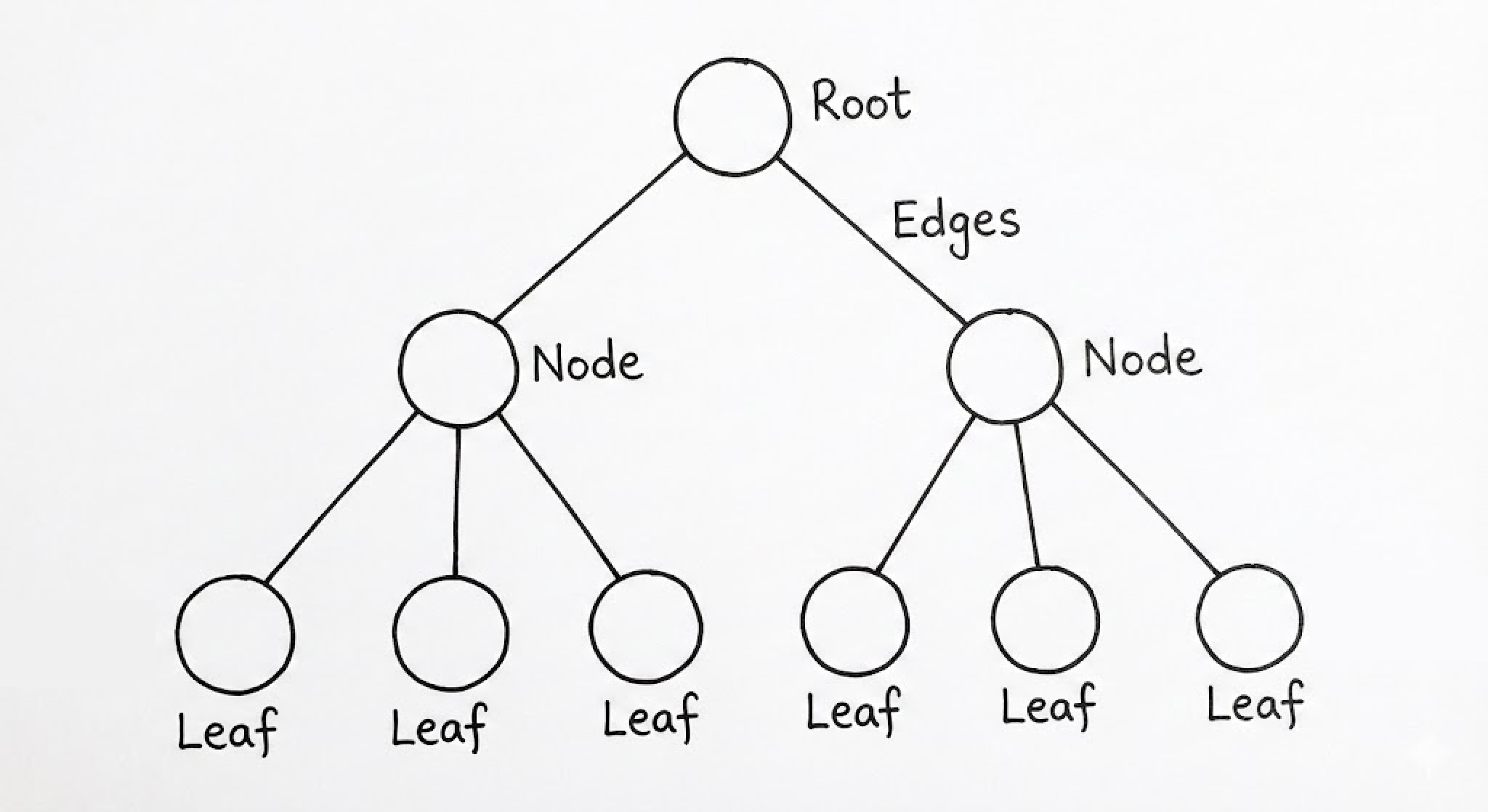
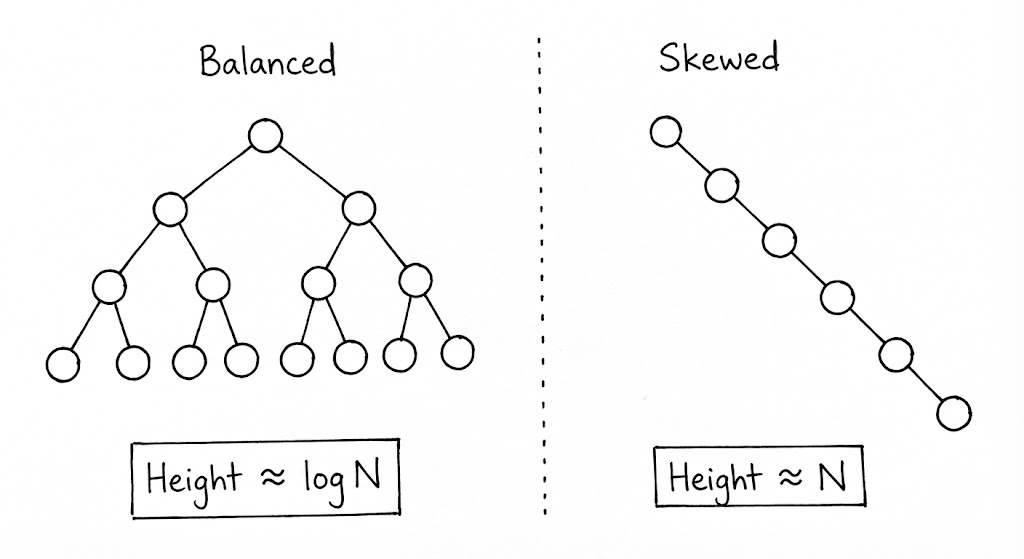
우리가 트리를 설계할 때 주목해야 할 지표는 ‘깊이(Depth)’와 ‘높이(Height)’입니다. 뿌리(Root)에서 특정 노드까지의 거리가 깊이라면, 해당 노드에서 가장 먼 잎(Leaf) 노드까지의 거리가 높이입니다. 이 수치들은 단순한 메트릭이 아니라, 알고리즘의 시간 복잡도를 결정짓는 물리적인 한계선입니다. 특히 현대 시스템에서 트리의 ‘편향성(Skewness)’은 엔지니어링의 적입니다. 균형이 깨진 트리는 사실상 연결 리스트와 다를 바 없으며, 이는 곧 캐시 효율성 저하와 탐색 성능의 타락으로 이어지기 때문입니다.
트리는 파일 시스템의 디렉토리 구조부터 HTML의 DOM Tree, 컴파일러의 추상 구문 트리(AST)에 이르기까지 질서가 필요한 모든 곳에 존재합니다. 이는 단순히 데이터를 저장하는 것을 넘어, 데이터가 가진 ‘맥락’과 ‘포함 관계’를 메모리 공간에 재현하려는 시도입니다. 우리는 이 비선형적 공간 위에서 재귀(Recursion)라는 도구를 휘둘러 복잡한 문제를 하위 문제로 쪼개고 정복해 나갑니다.
🧩 Node
트리는 노드(Node)라는 독립적인 개체들이 포인터로 얽혀 만들어진 거대한 유기체입니다. 하지만 우리는 종종 이 유기체의 가장 작은 단위인 ‘노드’ 자체의 물리적 무게를 간과하곤 합니다. 엔지니어링 관점에서 노드는 단순히 ‘데이터를 담는 그릇’을 넘어, 트리의 위상과 상태를 결정짓는 핵심 메타데이터의 집합체입니다. 노드가 어떤 정보를 품고 있느냐에 따라 트리의 성격이 단순한 탐색용 도구에서 고도의 자가 균형 시스템으로 진화합니다.
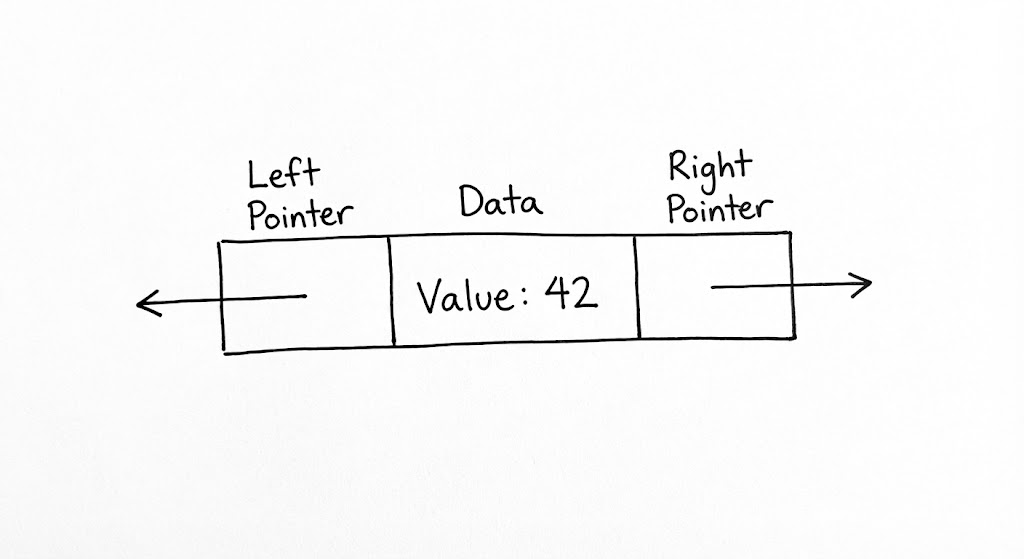
노드 하나가 메모리에서 차지하는 실질적인 공간을 계산해 보면 트리의 물리적 비용이 드러납니다. 현대의 64비트 시스템에서 부모 노드와 두 자식 노드(Left, Right)를 가리키는 포인터 세 개만으로도 이미 24바이트(8바이트 * 3)의 공간이 소모됩니다. 여기에 실제 데이터 필드와 메모리 정렬(Memory Alignment)을 위한 패딩(Padding)까지 고려하면, 정수 하나를 저장하기 위해 노드는 수 배에서 수십 배에 달하는 메모리 오버헤드를 감수해야 합니다. 이것이 바로 데이터가 수억 개 단위로 커질 때 트리가 배열에 비해 압도적인 메모리 점유율을 보이는 물리적 이유입니다.
하지만 이 오버헤드는 ‘지능’을 위한 정당한 대가입니다. 심화된 트리 구조로 나아갈수록 노드는 자신의 상태를 기록하기 위한 메타데이터를 품기 시작합니다. AVL 트리에서는 서브트리의 높이(Height)를, Red-Black 트리에서는 노드의 색상(Color) 정보를 관리합니다. 이 작은 데이터들이 모여 전체 트리의 균형을 실시간으로 감시하는 ‘센서’ 역할을 수행합니다. 숙련된 엔지니어는 이 메타데이터를 포인터의 남는 하위 비트에 숨기거나(Pointer Tagging), 구조체 필드 배치를 최적화하여 64바이트 캐시 라인(Cache Line) 하나에 최대한 많은 정보를 우겨넣는 설계를 고민해야 합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <stdint.h>
#include <stdbool.h>
/**
* * 1. __attribute__((aligned(32))):
* 현대 CPU의 L1 캐시 라인은 보통 64바이트입니다. 노드를 32바이트로 정렬함으로써
* 하나의 캐시 라인에 정확히 2개의 노드가 담기도록 유도합니다. 이는 CPU가 메모리에서
* 노드를 읽어올 때 인접한 노드까지 한 번에 캐시에 올릴 확률을 높여 성능을 최적화합니다.
* * 2. Pointer Tagging (uintptr_t left_and_color):
* 64비트 주소 체계에서 메모리는 8바이트 단위로 정렬되므로 주소값의 하위 3비트는 늘 0입니다.
* 이 '버려지는 1비트'를 활용해 Red-Black 트리의 색상 정보(RED/BLACK)를 인코딩합니다.
* 별도의 int 필드를 제거함으로써 노드 크기를 줄이고 데이터 밀집도를 높이는 전략입니다.
*/
typedef struct Node {
// 하위 1비트: 색상(0: BLACK, 1: RED), 나머지: 왼쪽 자식 주소
uintptr_t left_and_color;
struct Node *right;
struct Node *parent;
int32_t key;
// 32바이트 정렬을 맞추기 위한 패딩.
// 나중에 트리의 높이나 서브트리 크기를 저장하는 용도로 확장 가능합니다.
int32_t padding;
} __attribute__((aligned(32))) Node;
/* --- 비트 연산을 통한 포인터 및 메타데이터 추출 --- */
static inline Node* get_left(Node *n) {
// 마지막 1비트를 0으로 마스킹하여 순수한 메모리 주소만 확보합니다.
return (Node*)(n->left_and_color & ~1UL);
}
static inline bool is_red(Node *n) {
// 마지막 1비트만 추출하여 노드의 색상 상태를 즉시 판별합니다.
return (bool)(n->left_and_color & 1UL);
}
static inline void set_left(Node *n, Node *left_ptr, bool red) {
// 주소값과 색상 정보를 비트 합 연산으로 결합하여 단일 필드에 저장합니다.
n->left_and_color = (uintptr_t)left_ptr | (red ? 1UL : 0UL);
}
결국 노드를 설계한다는 것은 메모리 효율과 기능성 사이의 치열한 트레이드오프를 결정하는 일입니다. 힙(Heap) 메모리 곳곳에 파편화되어 흩어진 노드들은 CPU 입장에서는 ‘포인터 추적(Pointer Chasing)’이라는 고통스러운 여정을 강요합니다. 연속된 메모리를 점유하는 배열과 달리, 트리의 노드들은 캐시 지역성(Locality)을 파괴하기 쉽기 때문입니다. 따라서 고성능 시스템을 지향한다면, 개별 노드를 독립적으로 malloc 하기보다는 노드 풀(Node Pool)을 미리 할당하여 노드 간의 물리적 거리를 좁히는 전략이 필수적입니다.
부모 포인터 추가와 메모리 부담
노드에 부모 포인터(
parent)를 추가하면 트리 순회와 재균형 로직은 단순해지지만, 모든 노드의 크기가 8바이트씩 증가합니다. 수천만 개의 노드를 가진 시스템에서 이 8바이트는 결코 가볍지 않은 ‘성장통’으로 다가옵니다.
🧩 Pointer/Reference
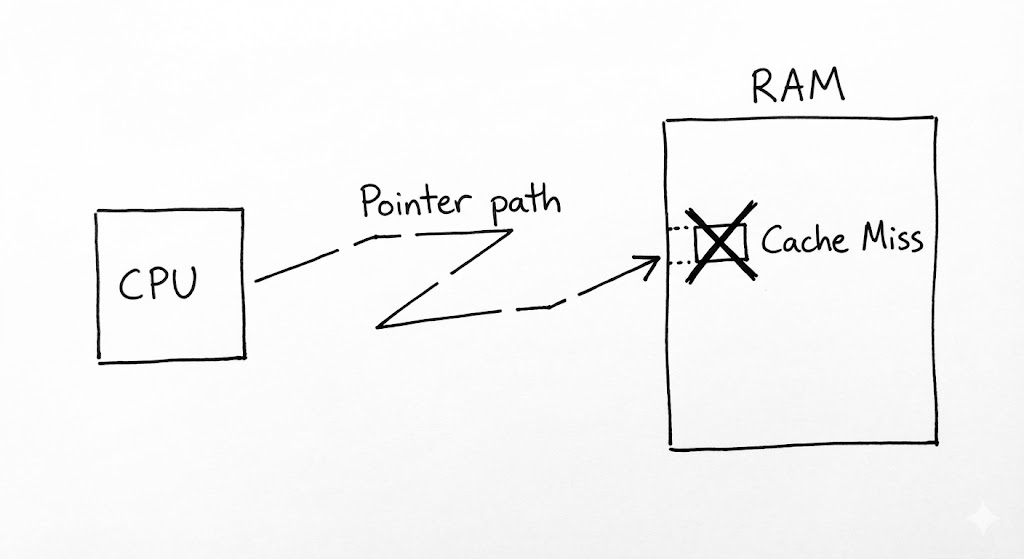
추상적인 자료구조 도식에서 우아한 화살표로 그려지는 ‘포인터(Pointer)’는 실제 물리 메모리 상에서는 64비트 정수 형태의 주소값에 불과합니다. 트리의 정체성을 형성하는 이 연결망은 논리적으로는 완벽한 계층을 만들어내지만, 하드웨어 계층으로 내려가는 순간 ‘포인터 추적(Pointer Chasing)’이라는 성능상의 거대한 비용을 발생시킵니다. 우리가 트리를 순회하며 노드를 하나씩 건너갈 때마다, CPU는 캐시 메모리에 존재하지 않는 무작위 주소를 읽어오기 위해 메인 메모리(RAM)로 향하는 비싼 여정을 떠나야 합니다.
현대 CPU 아키텍처는 데이터의 ‘지역성(Locality)’에 집착합니다. 배열처럼 데이터가 메모리에 연속적으로 배치되어 있으면, CPU는 다음에 읽을 데이터를 미리 짐작하여 L1, L2 캐시에 채워 넣습니다. 그러나 트리의 노드들은 힙(Heap) 공간 여기저기에 파편화되어 흩어져 있습니다. 부모 노드에서 자식 노드의 주소를 확인하고 그곳으로 점프하는 행위는 CPU의 프리페처(Prefetcher)를 무력화하며, 이는 심각한 캐시 미스(Cache Miss)로 이어집니다. 이론적인 시간 복잡도가 $O(\log N)$이라 할지라도, 실제 실행 시간(Wall-clock time)에서 트리가 때때로 배열 기반 구조보다 느리게 느껴지는 이유가 바로 여기에 있습니다.
이러한 하드웨어적 마찰을 극복하기 위해 엔지니어들은 ‘포인터의 추상화’를 물리적 인접성으로 치환하려는 시도를 멈추지 않습니다. 예를 들어, 이진 힙(Binary Heap)을 구현할 때 실제 포인터 대신 배열 인덱스($2i, 2i+1$)를 사용하는 것은 포인터 저장 공간을 아끼는 목적도 있지만, 데이터 간의 물리적 거리를 좁혀 캐시 적중률을 높이려는 고도의 전략입니다. 또한, 포인터 자체에 메타데이터를 숨기는 태그드 포인터(Tagged Pointer) 기법은 노드 객체로의 추가적인 메모리 접근 없이도 트리의 상태(예: Red-Black 트리의 색상)를 즉시 파악하게 해줍니다.
포인터는 트리의 ‘인대’와 같습니다. 인대가 없으면 뼈(Node)들이 모여 골격(Tree)을 유지할 수 없지만, 인대가 너무 길거나 복잡하게 얽히면 움직임은 둔탁해집니다. 따라서 트리를 설계할 때 우리는 단순히 논리적 연결의 정확성만을 따지는 수준을 넘어, 이 연결이 물리적 버스(Bus)를 타고 흐를 때 발생하는 전기적 신호의 지연까지 상상할 수 있어야 합니다.
대규모 트리의 포인터 추적 병목
포인터를 따라가는 작업은 현대 컴퓨팅에서 가장 느린 연산 중 하나입니다. 데이터가 작을 때는 문제가 되지 않지만, 수백만 개의 노드를 가진 거대 트리를 다룰 때는 ‘포인터 추적’이 전체 시스템 처리량(Throughput)의 병목이 됩니다.
🧩 Recursion
트리는 본질적으로 재귀적인 자료구조입니다. 하나의 노드는 그 자체로 작은 트리의 뿌리(Root)이며, 그 아래로 펼쳐진 왼쪽과 오른쪽 서브트리 역시 독립적인 트리의 속성을 완벽하게 유지합니다. 이러한 자가 유사성(Self-similarity) 덕분에 트리를 다루는 가장 우아하고 직관적인 언어는 ‘재귀(Recursion)’가 됩니다. 복잡한 전체 트리의 문제를 “현재 노드에서 할 일”과 “자식 노드에게 위임할 일”로 분리하는 순간, 수만 개의 노드로 구성된 미로 같던 데이터는 간결한 몇 줄의 코드로 통제됩니다.
하지만 이 우아한 논리 이면에는 시스템 호출 스택(Call Stack)이라는 물리적 비용이 숨어 있습니다. 재귀 함수가 자식 노드를 방문할 때마다 운영체제는 현재의 상태를 보존하기 위해 스택 프레임을 쌓아 올립니다. 트리의 높이가 깊어질수록 스택은 비대해지며, 만약 트리가 한쪽으로 심하게 치우친 편향 트리(Skewed Tree)라면 최악의 경우 스택 오버플로(Stack Overflow)를 발생시키며 프로세스를 중단시킵니다. 따라서 엔지니어는 재귀의 미학을 즐기되, 트리의 최대 높이($H$)가 시스템이 허용하는 스택의 한계를 넘지 않도록 보장하거나, 필요에 따라 루프와 명시적 스택(Explicit Stack)을 사용하는 반복문 형태로 로직을 전환하는 결단이 필요합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.function.Consumer;
public class TreeProcessor<T> {
static class Node<T> {
T data;
Node<T> left, right;
Node(T data) { this.data = data; }
}
/**
* 비재귀적 중위 순회 (Iterative In-order Traversal)
* * 시스템 호출 스택(Call Stack)의 한계를 극복하기 위해 힙 영역의 Deque를 사용합니다.
* 이는 수백만 층의 깊이를 가진 편향 트리에서도 StackOverflowError로부터 안전하며,
* ArrayDeque의 내부 배열 구조 덕분에 연결 리스트보다 나은 캐시 지역성을 제공합니다.
*/
public void traverseSafely(Node<T> root, Consumer<T> action) {
if (root == null) return;
// 명시적 스택은 시스템 스택보다 훨씬 거대한 메모리 영역(Heap)을 활용할 수 있습니다.
Deque<Node<T>> stack = new ArrayDeque<>();
Node<T> current = root;
while (current != null || !stack.isEmpty()) {
// 1. 현재 노드로부터 가장 왼쪽 리프까지 파고들며 경로를 스택에 적재
while (current != null) {
stack.push(current);
current = current.left;
}
// 2. 스택에서 노드를 꺼내 로직을 수행 (가장 최근에 추가된 왼쪽 끝 노드부터)
current = stack.pop();
action.accept(current.data);
// 3. 오른쪽 서브트리로 이동하여 다시 왼쪽 탐색을 반복
current = current.right;
}
}
}
트리 순회(Traversal)는 재귀적 사고가 가장 빛나는 지점입니다. 루트를 언제 방문하느냐에 따라 전위(Pre-order), 중위(In-order), 후위(Post-order) 순회로 나뉘며, 이는 단순한 순서의 차이를 넘어 데이터의 의미를 재구성합니다. 특히 이진 탐색 트리(BST)에서 중위 순회는 데이터를 오름차순으로 정렬된 스트림으로 변환하며, 후위 순회는 자식 노드의 상태를 먼저 확인해야 하는 폴더 용량 계산이나 수식 트리 평가에 최적화되어 있습니다.
또한, 우리는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 사이의 메모리 트레이드오프를 이해해야 합니다. 재귀를 이용한 DFS가 트리의 높이($H$)에 비례하는 스택 공간을 요구한다면, 큐(Queue)를 이용한 BFS는 트리의 최대 너비($W$)에 비례하는 메모리를 점유합니다. 아주 깊지만 폭이 좁은 트리에서는 BFS가 유리할 수 있고, 반대로 아주 넓지만 낮은 트리에서는 DFS가 메모리 측면에서 효율적입니다. 결국 재귀는 단순한 코딩 기법이 아니라, 데이터의 형상에 맞춰 시스템 자원을 어떻게 배분할 것인지를 결정하는 전략적 선택입니다.
재귀의 한계와 꼬리 재귀 최적화 (TCO)
많은 현대적 언어들이 꼬리 재귀 최적화를 지원하려고 노력하지만, 트리의 분기 구조(Branching) 특성상 완전한 최적화는 어렵습니다. 트리의 깊이가 예측 불가능할 정도로 깊다면, 재귀 대신 반복문과 사용자 정의 스택을 사용하여 힙(Heap) 영역을 활용하는 것이 안정성 면에서 탁월한 선택이 될 수 있습니다.
🧩 Balance Factor
균형 계수(Balance Factor)는 트리의 수명과 탐색 성능을 결정짓는 엔트로피의 척도입니다. 이진 탐색 트리(BST)가 선형 자료구조보다 압도적으로 빠른 이유는 데이터를 절반씩 버리며 후보군을 좁혀나가는 ‘분할 정복’의 논리에 기반하기 때문입니다. 하지만 이 논리는 트리가 좌우로 대칭을 이룬다는 가정하에만 유효합니다. 균형 계수는 바로 이 대칭성이 얼마나 유지되고 있는지를 나타내는 수치적 경고등입니다.
특정 노드 $n$에 대한 균형 계수 $BF(n)$은 다음과 같이 정의됩니다.
\[BF(n) = Height(left\_subtree) - Height(right\_subtree)\]이 수치가 0에 가까울수록 트리는 이상적인 이진 트리의 형태를 갖추며, 모든 탐색 경로는 $\log N$에 수렴합니다. 하지만 삽입과 삭제가 반복되면서 특정 방향으로 데이터가 쏠리기 시작하면 $BF$의 절대값은 커집니다. 엔지니어링 관점에서 가장 위험한 순간은 트리가 ‘편향(Skewed)’되는 지점입니다. 만약 모든 노드가 한쪽 자식만 가지게 되어 $BF$가 지속적으로 임계치를 넘는다면, 트리는 사실상 ‘연결 리스트’로 퇴화합니다. 이때 탐색 복잡도는 $O(\log N)$의 우아함을 잃고 $O(N)$의 선형 시간으로 타락하며, 이는 대규모 시스템에서 치명적인 레이턴시(Latency)를 유발합니다.
단순히 “균형이 중요하다”는 인식만으로는 부족합니다. 우리는 $BF$를 계산하기 위해 각 노드에 ‘높이(Height)’ 정보를 저장해야 할지, 아니면 연산 시점에 실시간으로 계산할지를 결정해야 합니다. 전자는 삽입/삭제 시마다 높이를 갱신해야 하는 오버헤드와 노드당 추가 메모리 공간을 요구하고, 후자는 $BF$를 확인하는 것 자체가 $O(N)$의 연산이 되어 배보다 배꼽이 더 커지는 결과를 초래합니다.
현대적인 자가 균형 트리들은 이 $BF$를 다루는 방식에서 갈라집니다. AVL 트리는 $|BF| \le 1$이라는 엄격한 규칙을 적용하여 탐색 성능을 극대화하는 반면, Red-Black 트리는 ‘색상’이라는 간접적인 지표를 통해 $BF$의 엄격함을 완화하고 대신 구조 변경 비용을 낮추는 트레이드오프를 선택합니다. 결국 균형 계수를 관리한다는 것은, 탐색의 효율성과 구조 유지의 비용 사이에서 최적의 평형점을 찾는 고도의 엔지니어링 의사결정 과정입니다.
트리의 균형이 깨지면 시스템에 어떤 일이 생길까?
$2^{20}$(약 100만 개)의 데이터를 가진 완전 이진 트리의 높이는 단 20에 불과합니다. 하지만 균형이 완전히 깨진 편향 트리의 높이는 1,000,000이 됩니다. 단 한 번의 조회를 위해 20번의 메모리 점프를 할 것인가, 100만 번의 점프를 할 것인가의 차이는 시스템의 생존을 결정짓습니다.
🧩 Rotation
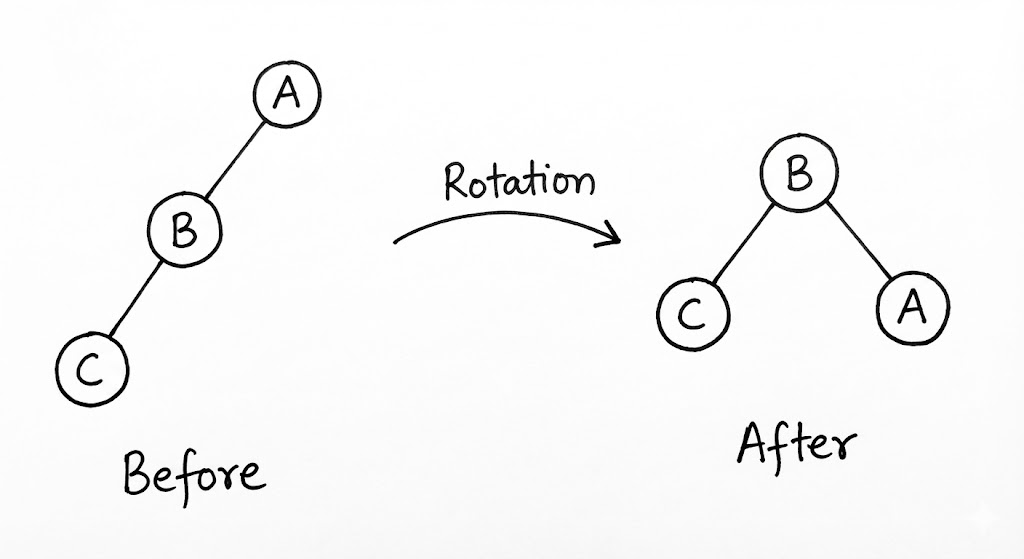
회전(Rotation)은 무너진 트리의 균형을 물리적으로 복구하는 ‘기하학적 수술’입니다. 균형 계수($BF$)가 임계치를 넘었을 때, 트리는 스스로의 구조를 비틀어 높이를 낮추고 탐색 효율을 되찾습니다. 이 과정의 아름다움은 노드 내부의 데이터를 옮기거나 복사하지 않고, 오직 노드 간의 ‘연결(Pointer)’을 재배치하는 것만으로 전체 시스템의 엔트로피를 낮춘다는 점에 있습니다.
회전은 불균형이 발생한 방향에 따라 네 가지 케이스로 분류되며, 크게 단일 회전과 이중 회전으로 나뉩니다.
단일 회전 (Single Rotation)
단일 회전은 편향이 한쪽 방향으로만 일어났을 때(LL 또는 RR) 수행됩니다. LL(Left-Left) 상황을 가정해 보겠습니다. 루트 노드의 왼쪽 자식의 왼쪽 서브트리가 너무 깊어졌을 때, 우리는 루트 노드를 ‘오른쪽’으로 끌어내립니다. 이때 기존의 왼쪽 자식이 새로운 루트가 되고, 기존 루트는 그의 오른쪽 자식으로 편입됩니다. 이 과정에서 기존 왼쪽 자식이 가지고 있던 오른쪽 서브트리는 기존 루트의 왼쪽 자식으로 자리를 옮기게 되는데, 이는 이진 탐색 트리의 대소 관계(Invariant)를 완벽하게 보존하는 우아한 이동입니다.
이중 회전 (Double Rotation)
데이터가 지그재그(LR 또는 RL) 형태로 꺾여 있을 때는 단일 회전만으로 균형을 맞출 수 없습니다. 이때는 두 번의 회전이 결합된 이중 회전이 필요합니다. 예를 들어 LR(Left-Right) 상황에서는 먼저 자식 노드 수준에서 좌회전(Left Rotation)을 수행하여 구조를 직선(LL) 형태로 펴준 뒤, 다시 루트 수준에서 우회전(Right Rotation)을 가해 전체 높이를 줄입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/**
* [Rotation의 위상 기하학적 정석]
* 회전은 노드의 위치를 바꾸는 것이 아니라, 서브트리의 주인을 교체하는 행위입니다.
* 이 과정에서 이진 탐색 트리(BST)의 불변성인 '왼쪽 < 루트 < 오른쪽' 관계는
* 단 한 순간도 깨지지 않으며, 오직 트리의 '높이'만이 재조정됩니다.
*/
public class TreeBalancer {
static class Node {
int key, height;
Node left, right;
Node(int key) { this.key = key; this.height = 1; }
}
/**
* 우회전 (Right Rotation - LL Case 해결)
* * 왼쪽으로 치우친(Left-Left) 구조를 오른쪽으로 끌어내려 균형을 맞춥니다.
* * 기존 루트의 왼쪽 자식이 새로운 루트가 되고,
* * 새로운 루트의 기존 오른쪽 서브트리는 이전 루트의 왼쪽 자식으로 편입됩니다.
*/
public Node rotateRight(Node y) {
Node x = y.left;
Node T2 = x.right;
// 1. 위상 재배치: x를 y의 부모로 승격
x.right = y;
y.left = T2;
// 2. 높이 갱신: 반드시 하위 노드(y)부터 갱신해야 전체 높이가 정확히 계산됩니다.
updateHeight(y);
updateHeight(x);
return x; // 새로운 부분 트리의 루트 반환
}
/**
* 좌회전 (Left Rotation - RR Case 해결)
* * 오른쪽으로 치우친(Right-Right) 구조를 왼쪽으로 당겨 높이를 낮춥니다.
*/
public Node rotateLeft(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
updateHeight(x);
updateHeight(y);
return y;
}
/**
* 이중 회전 (Double Rotation - LR Case 해결)
* * 지그재그 형태로 꺾인 구조는 단일 회전만으로 해결되지 않습니다.
* * 먼저 자식 수준에서 구조를 직선(LL)으로 편 뒤, 루트 수준에서 다시 회전합니다.
*/
public Node handleLR(Node node) {
// 1. 자식(왼쪽)을 좌회전하여 LL 형태로 변환
node.left = rotateLeft(node.left);
// 2. 전체를 우회전하여 균형 확보
return rotateRight(node);
}
private void updateHeight(Node n) {
n.height = 1 + Math.max(getHeight(n.left), getHeight(n.right));
}
private int getHeight(Node n) {
return n == null ? 0 : n.height;
}
}
엔지니어링 관점에서 회전 연산의 비용은 $O(1)$입니다. 단 3~4개의 포인터 변수 값을 교체하는 것만으로 수백만 개의 데이터를 품은 트리의 높이를 즉각적으로 제어할 수 있습니다. 하지만 회전이 일어나는 ‘시점’을 결정하기 위해 매 삽입/삭제마다 루트까지 거슬러 올라가며 $BF$를 확인하는 과정은 $O(\log N)$의 비용을 요구합니다. 결국 회전은 탐색의 안정성을 위해 지불하는 일종의 ‘보험료’와 같습니다.
포인터 업데이트 순서의 중요성
회전 코드 작성 시 가장 흔한 실수는 포인터 업데이트 순서를 잘못 지정하여 기존 노드의 주소값을 잃어버리는 ‘메모리 고립’ 현상입니다. 임시 변수를 활용해 연결 관계를 안전하게 보관한 뒤, 위상 기하학적 순서에 맞춰 연결을 교체해야 합니다.
AVL vs Red-Black
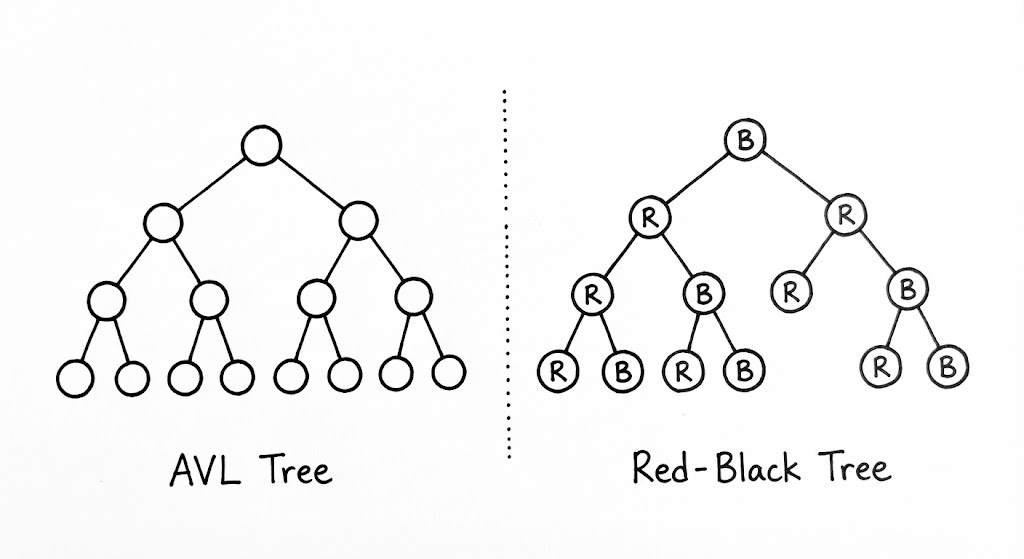
자가 균형 트리(Self-Balancing Tree)의 세계에서 AVL 트리와 Red-Black 트리는 각각 ‘완벽주의자’와 ‘실용주의자’라는 대조적인 정체성을 가집니다. 두 트리 모두 삽입과 삭제 시 발생할 수 있는 $O(N)$으로의 퇴행을 막기 위해 $O(\log N)$의 성능을 보장하지만, 그 성능을 달성하기 위해 지불하는 비용의 성격은 판이하게 다릅니다.
AVL 트리 (엄격한 질서)
AVL 트리는 ‘모든 노드의 자식 서브트리 높이 차이가 1을 넘지 않아야 한다’는 극도로 엄격한 규칙을 고수합니다. 이 규칙 덕분에 AVL 트리의 높이는 거의 항상 최소치에 가깝게 유지되며, 이는 곧 압도적인 탐색 성능으로 이어집니다. 하지만 이 완벽한 질서를 유지하기 위한 대가는 ‘잦은 회전’입니다. 데이터 하나가 삽입되거나 삭제될 때마다 균형이 깨질 확률이 높고, 그때마다 루트 노드까지 거슬러 올라가며 연쇄적인 회전 연산을 수행해야 합니다. 따라서 AVL 트리는 데이터의 변동이 적고 ‘조회(Lookup)’ 연산이 지배적인 환경에서 최적의 선택이 됩니다.
Red-Black 트리 (유연한 균형)
반면 Red-Black 트리는 노드에 ‘색상(Color)’이라는 메타데이터를 부여하고 5가지의 엄격한 불변성(Invariants)을 유지함으로써 균형을 맞춥니다. 핵심은 ‘루트에서 리프까지의 가장 긴 경로는 가장 짧은 경로의 두 배를 넘지 않는다’는 느슨한 보장입니다. AVL보다 조금 더 ‘치우친’ 상태를 허용하는 대신, 삽입과 삭제 시 발생하는 구조적 재배치(회전) 횟수를 획기적으로 줄였습니다.
RB-Tree는 회전 대신 색상을 반전시키는 ‘Color Flip’ 연산을 적극적으로 활용합니다. 색상 변경은 포인터 재배치보다 연산 비용이 저렴하며, 국소적인 수정만으로도 트리의 속성을 유지할 수 있는 경우가 많습니다. 이러한 특성 덕분에 Java의 TreeMap, C++의 std::set, 그리고 리눅스 커널의 완전 공평 스케줄러(CFS)처럼 삽입과 삭제가 빈번하게 일어나는 범용적인 시스템에서 표준으로 자리 잡았습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
* 1. 색상 반전(Color Flip) vs. 회전(Rotation):
* 색상 변경은 단순한 비트 수정 연산으로, 포인터 세 개를 바꿔야 하는 회전보다 비용이 저렴합니다.
* Red-Black 트리는 가능한 한 색상 변경으로 균형을 해결하려 시도하며,
* 이것이 AVL 트리보다 삽입/삭제 성능이 우수한 근본적인 이유입니다.
* 2. Invariant 유지:
* 삽입된 노드를 RED로 설정하여 검은 노드의 개수(Black-height)를 유지하되,
* 연속된 RED 노드가 발생하는 상황을 국소적인 회전과 색상 반전으로 해결합니다.
*/
public class RedBlackBalancer {
private static final boolean RED = true;
private static final boolean BLACK = false;
private void fixAfterInsertion(Node x) {
x.color = RED;
// 부모가 RED일 때만 속성이 깨지므로, 루트까지 올라가며 수정합니다.
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Node uncle = rightOf(parentOf(parentOf(x)));
if (colorOf(uncle) == RED) {
// Case 1: 삼촌이 RED인 경우 - 색상 반전만으로 해결 가능
// 할아버지 노드를 RED로 만들고 위쪽에서 다시 검사합니다.
setColor(parentOf(x), BLACK);
setColor(uncle, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
// Case 2: 삼촌이 BLACK이고 x가 오른쪽 자식 (지그재그)
// 좌회전을 통해 Case 3(직선 형태)으로 변환합니다.
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// Case 3: 삼촌이 BLACK이고 x가 왼쪽 자식 (직선)
// 부모와 할아버지의 색상을 바꾸고 우회전하여 균형을 확정합니다.
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
// 오른쪽 대칭 케이스 (동일한 논리 적용)
// ... (생략)
}
}
root.color = BLACK; // 루트는 항상 BLACK이어야 한다는 불변성을 마지막에 강제합니다.
}
}
탐색인가, 갱신인가
결국 두 트리의 선택은 “어디에서 병목을 감수할 것인가?”의 문제로 귀결됩니다.
- 조회 중심(Read-Heavy): 사전(Dictionary) 검색이나 고정된 데이터셋의 인덱싱에는 높이가 더 낮은 AVL 트리가 유리합니다.
- 갱신 중심(Write-Heavy): 실시간으로 데이터가 추가되고 삭제되는 메모리 관리자나 이벤트 큐에서는 업데이트 오버헤드가 적은 Red-Black 트리가 압승입니다.
우리는 추상적인 $O(\log N)$이라는 기호 뒤에 숨겨진 ‘상수 시간의 미학’을 이해해야 합니다. AVL의 회전 상수가 큰지, RB-Tree의 경로 탐색 상수가 큰지를 결정하는 것은 결국 우리가 다루는 데이터의 흐름과 시스템의 성격입니다.
왜 RB-Tree가 더 흔할까?
대다수 실무 환경에서는 데이터의 ‘조회’만큼이나 ‘생성’과 ‘소멸’의 비용이 시스템 전체 처리량(Throughput)에 큰 영향을 미칩니다. RB-Tree는 최악의 상황에서도 안정적인 쓰기 성능을 제공하기에, 엔지니어들에게 더 신뢰받는 범용 도구가 되었습니다.
B-Tree
우리가 앞서 다룬 AVL이나 Red-Black 트리는 모두 ‘메모리 내(In-Memory)’ 환경을 가정합니다. 하지만 데이터의 규모가 테라바이트 단위로 커져 디스크에 인덱스를 저장해야 하는 순간, 이진 트리의 우아함은 ‘디스크 레이턴시’라는 물리적 장벽에 부딪혀 산산조각 납니다. 메모리 접근이 나노초(ns) 단위인 데 반해 디스크 탐색(Seek)은 밀리초(ms) 단위의 시간을 요구합니다. 이진 트리에서 100만 개의 데이터를 찾기 위해 20번의 노드를 거친다는 것은, 곧 20번의 디스크 I/O가 발생할 수 있음을 의미하며 이는 현대 시스템에서 수용 불가능한 지연을 초래합니다.
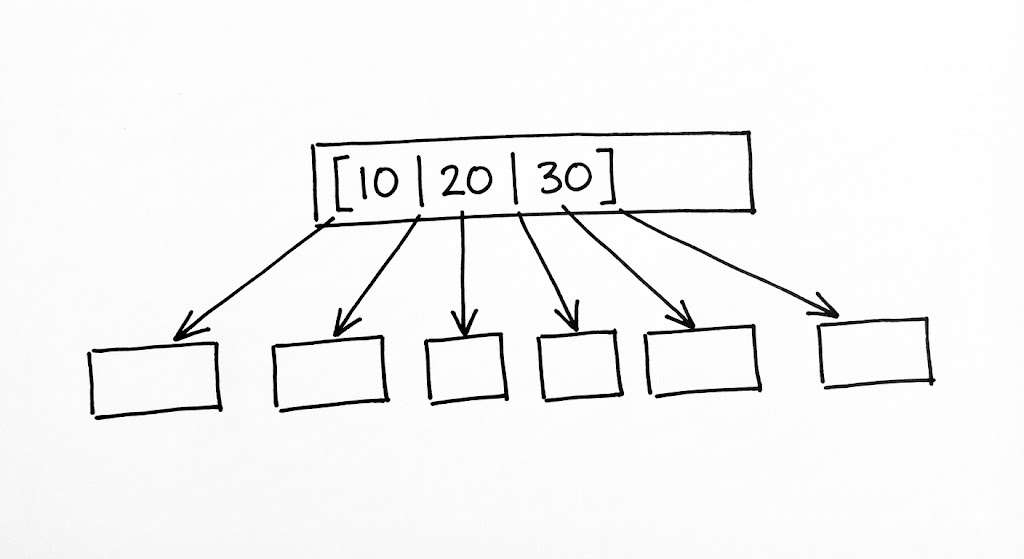
B-Tree는 이러한 하드웨어적 한계를 극복하기 위해 ‘차수(Degree)’를 높이는 전략을 취합니다. 하나의 노드에 단 하나의 키만 담는 이진 트리와 달리, B-Tree의 노드는 수십, 수백 개의 키를 배열 형태로 품고 있습니다. 이를 통해 트리의 높이를 획기적으로 낮춥니다(Fan-out). 예를 들어 차수가 100인 B-Tree는 단 3~4개의 층만으로도 수억 개의 데이터를 수용할 수 있습니다. 이는 단 3~4번의 디스크 접근만으로 원하는 데이터가 포함된 ‘페이지(Page)’를 찾아낼 수 있음을 의미합니다.
상향식 성장(Bottom-up Growth)
B-Tree의 가장 경이로운 점은 그 균형 유지 메커니즘에 있습니다. 이진 트리가 루트에서 아래로 뻗어 나가는 것과 달리, B-Tree는 ‘리프(Leaf) 노드’에서 시작하여 위로 솟구치며 성장합니다. 모든 리프 노드가 동일한 깊이에 위치한다는 불변성(Invariant)을 지키기 위해, B-Tree는 노드 분할(Split)이라는 독특한 연산을 수행합니다.
특정 노드에 데이터가 가득 차면(Max Keys), 해당 노드는 두 개로 쪼개지고 중간값(Median)이 부모 노드로 승격(Promote)됩니다. 만약 부모 노드마저 가득 차 있다면 이 과정은 루트 노드까지 연쇄적으로 일어날 수 있으며, 루트 노드가 쪼개질 때만 트리의 전체 높이가 1 증가합니다. 이러한 ‘상향식 전파’ 덕분에 B-Tree는 데이터의 삽입 순서와 상관없이 항상 완벽하게 균형 잡힌 계층을 유지합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/**
* 1. Fan-out 극대화:
* 이진 트리와 달리 하나의 노드에 수백 개의 키를 담아 트리의 높이를 압축합니다.
* 이는 디스크 I/O 횟수를 결정짓는 '로그의 밑'을 키워 물리적 지연을 극복하는 전략입니다.
* 2. Bottom-up Growth (상향식 성장):
* B-Tree는 리프에서 가득 찬 노드를 쪼개고 중간값을 부모로 승격(Promote)시키며 위로 자랍니다.
* 이 '분할' 과정이 루트까지 도달했을 때만 트리의 전체 높이가 증가하며,
* 이를 통해 모든 리프 노드가 항상 동일한 깊이를 유지하는 완벽한 균형을 달성합니다.
*/
public class BTreeManager {
private final int T; // 최소 차수 (Minimum Degree)
public BTreeManager(int t) {
this.T = t;
}
/**
* 가득 찬 자식 노드를 분할하여 부모 노드에 공간을 확보합니다.
* @param parent 분할될 노드의 부모
* @param i parent의 자식들 중 분할할 자식의 인덱스
* @param fullNode 가득 찬(keys == 2T-1) 자식 노드
*/
public void splitChild(Node parent, int i, Node fullNode) {
// 1. 가득 찬 노드의 후반부 키(T-1개)를 담을 새 노드 생성
Node newNode = new Node(fullNode.isLeaf);
newNode.keyCount = T - 1;
// 2. 중간값 이후의 키들을 새 노드로 복사
for (int j = 0; j < T - 1; j++) {
newNode.keys[j] = fullNode.keys[j + T];
}
// 3. 리프 노드가 아니라면 자식 포인터들도 함께 이동
if (!fullNode.isLeaf) {
for (int j = 0; j < T; j++) {
newNode.children[j] = fullNode.children[j + T];
}
}
// 4. 기존 노드의 키 개수를 절반으로 축소
fullNode.keyCount = T - 1;
// 5. 부모 노드에 새 자식 노드를 위한 포인터 공간 확보
for (int j = parent.keyCount; j >= i + 1; j--) {
parent.children[j + 1] = parent.children[j];
}
parent.children[i + 1] = newNode;
// 6. 부모 노드에 가득 찬 노드의 중간값(Median)을 승격시켜 삽입
for (int j = parent.keyCount - 1; j >= i; j--) {
parent.keys[j + 1] = parent.keys[j];
}
parent.keys[i] = fullNode.keys[T - 1];
parent.keyCount++;
}
}
페이지와 블록
현대 데이터베이스(PostgreSQL, MySQL InnoDB 등)가 사용하는 B+Tree는 여기서 한 걸음 더 나갑니다. 내부 노드(Internal Node)에는 탐색을 위한 ‘가이드(Key)’만 남겨두고, 실제 데이터나 레코드 포인터는 모두 리프 노드에만 저장합니다. 또한 리프 노드들을 연결 리스트로 이어 ‘범위 스캔(Range Scan)’ 성능을 극대화합니다.
이는 운영체제의 파일 시스템이 데이터를 ‘블록(Block)’ 단위로 읽어온다는 점을 완벽히 이용한 설계입니다. 노드 하나의 크기를 디스크 페이지 크기(보통 16KB)에 맞춤으로써, 한 번의 I/O로 최대한 많은 인덱스 정보를 CPU 캐시로 끌어올리는 것입니다. 결국 B-Tree는 수학적 추상화를 넘어, 하드웨어의 물리적 특성을 소프트웨어 구조로 정복해낸 엔지니어링의 승리라고 할 수 있습니다.
왜 $O(\log N)$은 충분하지 않은가?
알고리즘 시험에서는 $O(\log N)$이면 충분할지 모르지만, 실전 인덱싱에서는 로그의 ‘밑(Base)’이 중요합니다. 밑이 2인 이진 트리와 밑이 128인 B-Tree 사이에는 실제 성능 면에서 거대한 ‘물리적 심연’이 존재합니다.
Segment Tree
우리가 지금까지 다룬 트리들이 ‘특정 값’을 빠르게 찾는 데 집중했다면, 세그먼트 트리(Segment Tree)는 ‘특정 구간’의 요약 정보를 빛의 속도로 추출하기 위해 설계된 특수 병기입니다. 배열의 $L$부터 $R$까지의 합이나 최댓값을 구해야 하는 상황을 가정해 봅시다. 단순 루프($O(N)$)는 데이터가 빈번히 수정되는 환경에서 치명적인 병목이 됩니다. 세그먼트 트리는 이 선형적인 구간을 재귀적으로 쪼개어 각 노드에 해당 구간의 ‘대표값’을 미리 계산해 두는 방식으로 $O(\log N)$의 기적을 만들어냅니다.
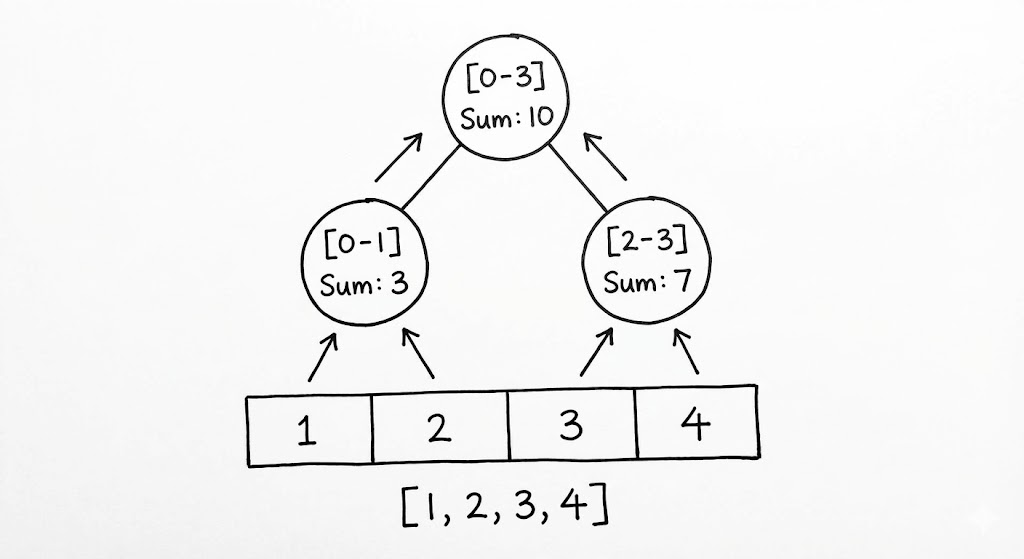
세그먼트 트리의 아름다움은 그 구조적 간결함에 있습니다. 리프 노드에는 배열의 개별 원소들이 자리하고, 부모 노드는 두 자식 노드가 담당하는 구간의 합(또는 최댓값)을 품습니다. 이를 통해 우리는 거대한 배열의 어떤 구간이라도 단 $2 \log N$개 이내의 노드 조합만으로 완벽하게 설명할 수 있습니다. 이는 마치 전국 지도를 시/도, 시/군/구 단위로 계층화하여 특정 지역의 인구 통계를 즉각 산출하는 체계와 같습니다.
Lazy Propagation
데이터의 수정이 빈번한 환경에서 세그먼트 트리는 또 하나의 도전에 직면합니다. 구간 전체($L$ to $R$)에 특정 값을 더해야 할 때, 모든 관련 노드를 즉시 갱신하는 것은 다시 $O(N)$의 늪으로 빠지는 길입니다. 여기서 엔지니어들은 ‘지연 전파(Lazy Propagation)’라는 고도의 전략을 도입합니다. 당장 필요하지 않은 하위 노드의 갱신을 미루고, 해당 정보를 ‘Lazy’ 배열에 기록해 두었다가 나중에 그 노드를 실제로 방문할 때 비로소 업데이트를 수행하는 방식입니다.
이는 ‘필요할 때까지만 일을 미루는’ 지능적인 게으름입니다. 이 메커니즘 덕분에 구간 업데이트조차 $O(\log N)$으로 억제되며, 세그먼트 트리는 실시간 주식 차트의 이동평균선 계산이나 대규모 그래픽 렌더링의 구간 연산 등 극한의 성능이 요구되는 지점에서 대체 불가능한 도구로 군림합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/**
* 1. 구간의 계층적 압축:
* 배열의 각 원소를 리프 노드에 두고, 상위 노드로 갈수록 해당 구간의 '합'이나 '최댓값'을
* 미리 계산하여 저장합니다. 이를 통해 어떤 임의의 구간 [L, R]에 대한 쿼리도
* 단 2 * log N개 이내의 노드 조합으로 해결합니다.
* 2. Lazy Propagation (지연 전파):
* 특정 구간 전체에 값을 더하는 업데이트가 발생했을 때, 당장 조회되지 않는 하위 노드까지
* 즉시 수정하는 것은 낭비입니다. 'Lazy' 배열에 수정 사항을 기록해 두었다가,
* 나중에 해당 노드를 실제로 방문할 때 비로소 업데이트를 수행하는 '지능적인 게으름'을 구현합니다.
*/
public class LazySegmentTree {
private long[] tree;
private long[] lazy;
private int n;
public LazySegmentTree(int[] arr) {
this.n = arr.length;
// 안전한 모든 노드 수용을 위해 4N 크기의 메모리를 할당하는 '4N의 법칙'을 따릅니다.
this.tree = new long[4 * n];
this.lazy = new long[4 * n];
build(arr, 1, 0, n - 1);
}
private void build(int[] arr, int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
build(arr, 2 * node, start, mid);
build(arr, 2 * node + 1, mid + 1, end);
tree[node] = tree[2 * node] + tree[2 * node + 1];
}
/**
* 구간 업데이트: [l, r] 범위에 val을 더함 (O(log N))
*/
public void updateRange(int node, int start, int end, int l, int r, long val) {
// 현재 노드에 미뤄둔 작업이 있다면 자식에게 전파하고 현재 노드를 갱신합니다.
push(node, start, end);
if (start > end || start > r || end < l) return;
// 현재 구간이 업데이트 범위에 완전히 포함되면, 더 내려가지 않고 기록만 남깁니다.
if (start >= l && end <= r) {
lazy[node] += val;
push(node, start, end);
return;
}
int mid = (start + end) / 2;
updateRange(node * 2, start, mid, l, r, val);
updateRange(node * 2 + 1, mid + 1, end, l, r, val);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
/**
* 지연된 값을 실제 노드에 반영하고 자식에게 책임을 넘기는 'Push' 메커니즘
*/
private void push(int node, int start, int end) {
if (lazy[node] != 0) {
// 구간 크기만큼 값을 한꺼번에 반영하여 O(1)에 처리를 끝냅니다.
tree[node] += (end - start + 1) * lazy[node];
if (start != end) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
public long query(int node, int start, int end, int l, int r) {
push(node, start, end);
if (start > end || start > r || end < l) return 0;
if (l <= start && end <= r) return tree[node];
int mid = (start + end) / 2;
return query(node * 2, start, mid, l, r) + query(node * 2 + 1, mid + 1, end, l, r);
}
}
배열 기반 구현의 미학
흥미롭게도 세그먼트 트리는 포인터 대신 배열 인덱싱을 통해 구현되는 경우가 많습니다. $i$번 노드의 자식이 $2i$와 $2i+1$에 위치한다는 규칙을 활용하면, 포인터 추적으로 인한 캐시 미스를 최소화하고 메모리 레이아웃을 극도로 정갈하게 유지할 수 있습니다. 이는 트리의 논리를 유지하면서도 하드웨어 효율성을 극대화하려는 엔지니어링적 절충안의 정수입니다.
4N의 법칙
세그먼트 트리를 배열로 구현할 때, 안전하게 모든 노드를 수용하기 위해서는 원본 배열 크기의 4배에 달하는 공간이 필요합니다. 메모리를 조금 더 지불하더라도 포인터 연산의 복잡도를 제거하고 $O(\log N)$의 안정성을 확보하겠다는 단호한 트레이드오프입니다.
Summary
트리는 단순히 데이터를 계층적으로 저장하는 수단을 넘어, 하드웨어의 물리적 한계와 데이터의 복잡성 사이에서 최적의 균형을 찾아내려는 엔지니어링 의사결정의 집약체입니다. 우리는 메모리 파편화와 포인터 추적이라는 비용을 지불하며 AVL과 Red-Black 트리의 자가 균형 로직을 얻었고, 디스크 I/O라는 거대한 벽을 넘기 위해 B-Tree의 다차원 분기 전략을 채택했습니다. 나아가 세그먼트 트리와 같은 변형 구조는 지연 전파라는 영리한 기법을 통해 동적인 구간 정보까지 $O(\log N)$의 영역으로 끌어들였습니다. 결국 좋은 엔지니어링이란 주어진 데이터의 흐름과 하드웨어 환경에 가장 적합한 ‘트리의 형상’을 선택하고 구현하는 일입니다. 이 질서 정연한 디지털 신경망은 현대 컴퓨팅 시스템이 거대한 데이터를 지능적으로 다룰 수 있게 만드는 가장 강력한 기반으로 남을 것입니다.