[Distributed System] Logical Time과 Vector Clock
우리는 ‘지금 이 순간’이라는 개념이 우주 어디에서나 보편적이라고 믿는 경향이 있습니다. 하지만 분산 시스템의 세계에 발을 들이는 순간, 이 직관은 가장 먼저 무너져야 할 허상입니다. 서로 떨어진 두 서버가 “정확히 같은 시간”에 데이터를 수정했다고 주장할 때, 그 ‘동시성’을 입증할 수 있는 절대적인 기준점은 존재하지 않습니다.
흔히 우리는 NTP(Network Time Protocol)를 통해 서버 간의 시간을 동기화하면 문제가 해결될 것이라 착각합니다. 하지만 네트워크 패킷이 전달되는 시간은 일정하지 않으며, 수정처럼 맑은 정밀도를 기대하는 하드웨어 클록조차 온도와 전압의 미세한 변화에 따라 ‘클록 드리프트(Clock Drift)’라 불리는 시간 왜곡을 일으킵니다.
물리적 시계의 한계
GPS 시스템은 원자시계의 나노초 단위 정밀도에 의존하며, 단 1나노초의 오차만으로도 지상에서는 약 30cm의 위치 오차를 발생시킵니다. 이토록 정밀하게 설계된 시스템조차 상대성 이론에 따른 시간 왜곡을 보정해야만 작동합니다. 하물며 퍼블릭 클라우드의 가상 머신 위에서 돌아가는 일반적인 서버들이 수 밀리초(ms) 단위의 네트워크 지연 속에서 ‘절대적 순서’를 맞추는 것은 물리적으로 불가능에 가깝습니다.
분산 시스템에서 발생하는 결정적인 문제는 ‘물리적 시간’이 사건의 ‘인과 관계(Causality)’를 보장하지 못한다는 점입니다. A 서버에서 10시 0분 1초에 발생한 이벤트가 B 서버에 전달되었을 때, B 서버의 시계가 아주 미세하게 느리다면 B는 이 이벤트를 10시 0분 0초에 일어난 것으로 기록할 수 있습니다. 결과가 원인보다 앞서는 시간 역전 현상, 즉 ‘인과적 모순’이 발생하는 것입니다.
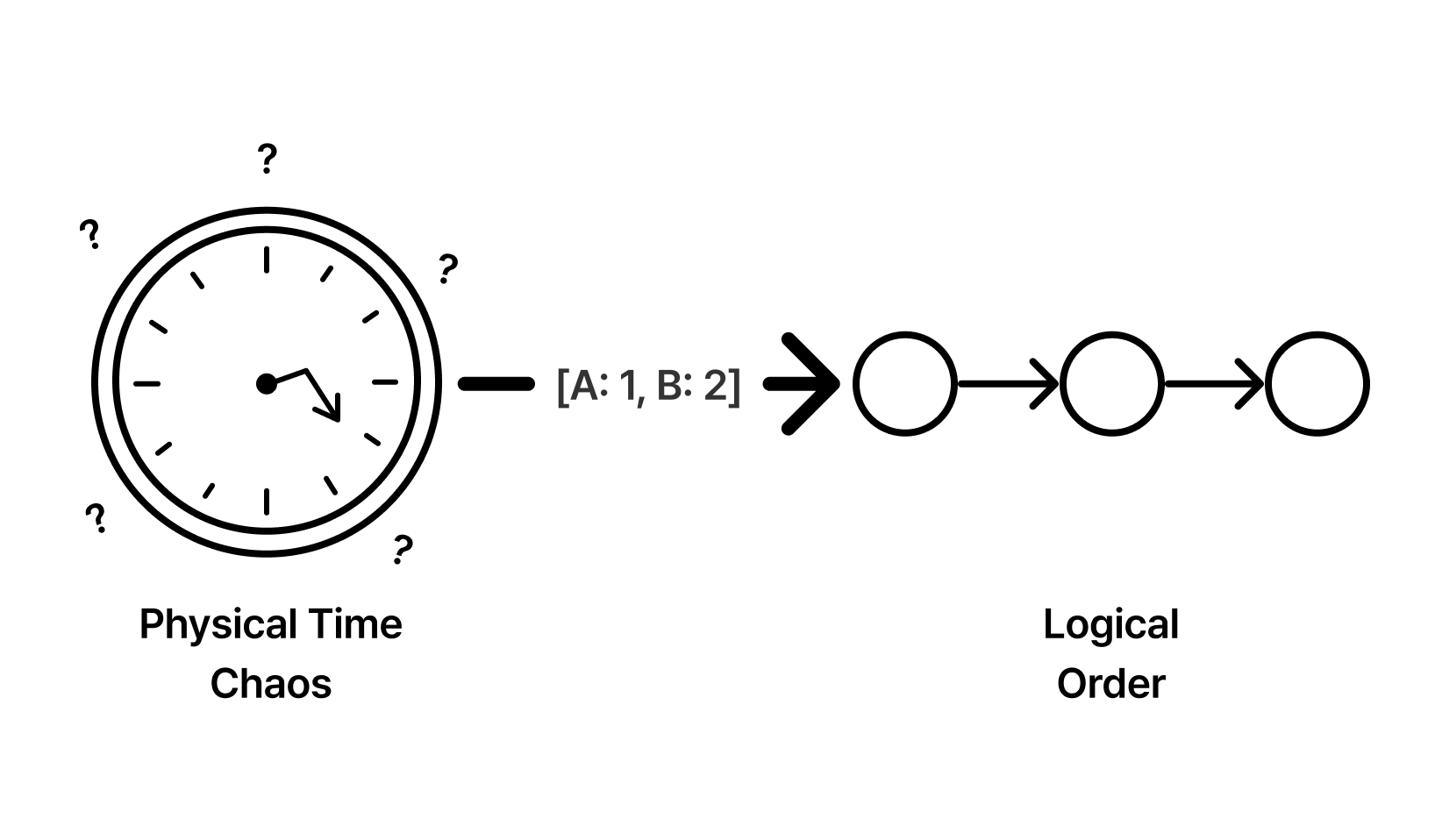
결국 우리는 질문을 바꿔야 합니다. “지금 몇 시인가?”가 아니라, “이 사건이 저 사건보다 먼저 일어났음을 어떻게 증명할 것인가?”에 집중해야 합니다. 이것이 바로 우리가 물리적 시계의 숫자를 버리고, 논리적 시간(Logical Time)이라는 추상적인 항해 일지를 작성해야 하는 이유입니다.
🧩 Logical Time
물리적 시계가 신뢰를 잃은 자리에서 레슬리 램포트(Leslie Lamport)는 새로운 질서를 제안했습니다. 그는 “시간이란 무엇인가”라는 형이상학적 질문 대신, “사건들 사이의 인과 관계를 어떻게 정의할 것인가”라는 실용적 문제에 집중했습니다. 이것이 바로 논리적 시간(Logical Time)의 탄생입니다. 여기서 시간은 시계 바늘의 움직임이 아니라, 사건과 사건 사이의 ‘인과적 선후 관계’를 나타내는 일련번호로 치환됩니다.
Happened-before 관계
논리적 시간의 핵심은 ‘Happened-before’라고 불리는 이항 관계($\rightarrow$)입니다. 이 관계는 다음 세 가지 직관적인 규칙을 통해 정의됩니다.
- 동일 프로세스 내의 순서: 같은 프로세스 내에서 사건 $a$가 사건 $b$보다 먼저 발생했다면, $a \rightarrow b$입니다.
- 메시지 전송과 수신: 프로세스 A가 메시지를 보내는 사건이 $a$이고, 프로세스 B가 해당 메시지를 받는 사건이 $b$라면, $a \rightarrow b$입니다. 원인이 결과보다 먼저 일어나야 한다는 자명한 법칙입니다.
- 이행성(Transitivity): $a \rightarrow b$이고 $b \rightarrow c$이면, $a \rightarrow c$입니다.
만약 두 사건 사이에 어떠한 경로로도 $a \rightarrow b$나 $b \rightarrow a$가 성립하지 않는다면, 우리는 이 두 사건이 동시적(Concurrent)이라고 부릅니다. 이는 물리적으로 동시에 일어났다는 뜻이 아니라, 서로에게 아무런 영향을 주지 않았다는 ‘인과적 무관함’을 의미합니다.
램포트 클럭 알고리즘과 메커니즘
램포트 시계는 각 프로세스가 내부에 정수 카운터를 유지하는 단순한 메커니즘으로 작동합니다. 복잡한 동기화 장치 없이도 네트워크 메시지만으로 전체 시스템의 인과 관계를 추적할 수 있다는 점이 이 알고리즘의 우아함입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import java.util.concurrent.atomic.AtomicLong;
/**
* 인과 관계의 부분 순서를 보장하는 논리적 시계
*/
public class LamportClock {
private final AtomicLong counter = new AtomicLong(0);
// 내부 이벤트 발생 시: 카운터를 1 증가
public long tick() {
return counter.incrementAndGet();
}
// 메시지 송신 시: tick 후 현재 값을 메시지에 담아 보냄
public long send() {
return tick();
}
// 메시지 수신 시: max(로컬, 수신값) + 1로 갱신
public void receive(long receivedTimestamp) {
counter.updateAndGet(current -> Math.max(current, receivedTimestamp) + 1);
}
public long getTime() {
return counter.get();
}
}
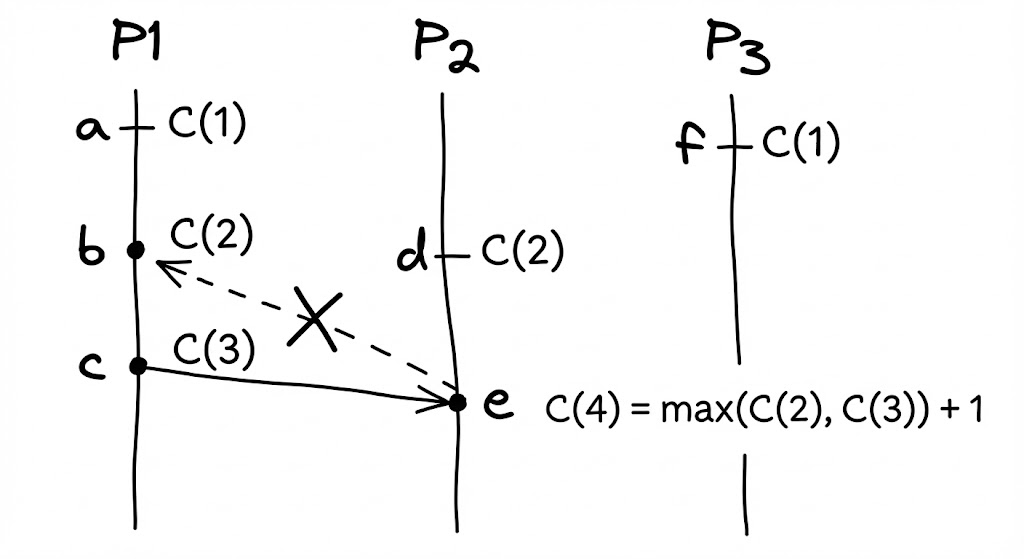
알고리즘의 실행 단계는 다음과 같습니다.
- 프로세스 내에서 이벤트가 발생할 때마다 로컬 카운터를 1 증가시킵니다.
- 메시지를 보낼 때, 현재의 로컬 카운터 값을 메시지에 포함하여 전송합니다.
- 메시지를 받을 때,
max(로컬 카운터, 받은 타임스탬프) + 1로 자신의 카운터를 갱신합니다.
역은 성립하지 않는다
램포트 시계는 강력하지만 치명적인 논리적 빈틈을 가지고 있습니다. 램포트 타임스탬프를 $C(x)$라고 할 때, 다음 명제는 참입니다.
$a \rightarrow b$ 이면 $C(a) < C(b)$ 이다.
하지만 이 명제의 역(Converse)은 성립하지 않습니다. 즉, $C(a) < C(b)$라고 해서 반드시 $a$가 $b$의 원인이라고 단정할 수 없습니다. 단순히 우연히 다른 타임라인에서 낮은 숫자를 부여받았을 뿐, 두 사건은 서로를 모르는 ‘동시적’ 관계일 수 있기 때문입니다.
Partial vs Total Ordering
램포트 시계는 인과 관계를 보존하는 ‘부분 순서’를 제공합니다. 여기에 프로세스 ID와 같은 고유 식별자를 추가하면 모든 사건에 고유한 순서를 매기는 ‘전체 순서’를 만들 수 있습니다. 하지만 이 숫자가 ‘진짜 인과 관계’를 뜻하는지는 여전히 알 수 없습니다. 이 숫자의 간극을 메우고, 숫자가 낮으면 정말 원인이었는지를 판별하기 위해 우리는 벡터 클럭이라는 더 고차원적인 도구가 필요하게 됩니다.
🧩 Vector Clock
램포트 시계는 ‘A가 B의 원인이라면 $C(A) < C(B)$이다’라는 명제를 증명했지만, 그 역인 ‘타임스탬프가 작으면 원인이다’라는 명제는 증명하지 못했습니다. 이는 분산 시스템에서 데이터 충돌을 감지해야 하는 엔지니어들에게 치명적인 약점이었습니다. 타임스탬프 숫자만 보고는 두 사건이 선후 관계인지, 아니면 서로의 존재를 모른 채 각자 발생한 ‘동시적’ 사건인지 알 길이 없었기 때문입니다.
이 논리적 공백을 메우기 위해 등장한 것이 바로 벡터 클럭(Vector Clock)입니다. 벡터 클럭은 단일 숫자가 아닌, 시스템 내 모든 프로세스의 상태를 담은 ‘벡터(배열)’를 주고받음으로써 인과 관계를 완벽하게 추적합니다.
스칼라에서 벡터로
벡터 클럭의 핵심 아이디어는 간단합니다. “내가 아는 시간뿐만 아니라, 내가 아는 다른 모든 이들의 시간까지 기록한다”는 것입니다. $N$개의 프로세스가 있는 시스템에서 각 프로세스는 크기가 $N$인 정수 배열 $V$를 유지합니다. 여기서 $V[i]$는 프로세스 $P_i$가 지금까지 발생시킨 이벤트의 개수를 의미합니다.
이 다차원적인 기록 방식 덕분에, 벡터 클럭은 시스템 전체의 지식 상태를 스냅샷처럼 포착합니다. 어떤 메시지를 받았을 때 그 메시지에 담긴 벡터를 보면, 송신자가 메시지를 보내기 직전까지 다른 프로세스들에 대해 어디까지 알고 있었는지를 정확히 파악할 수 있습니다.
벡터 클럭의 작동 원리
벡터 클럭은 다음의 세 가지 규칙에 따라 엄격하게 갱신됩니다.
- 로컬 이벤트: 프로세스 $P_i$에서 이벤트가 발생하면, 자신의 인덱스 값을 증가시킵니다: $V_i[i] = V_i[i] + 1$.
- 메시지 전송: 메시지를 보낼 때, 현재 자신의 벡터 전체 $V_i$를 메시지에 실어 보냅니다.
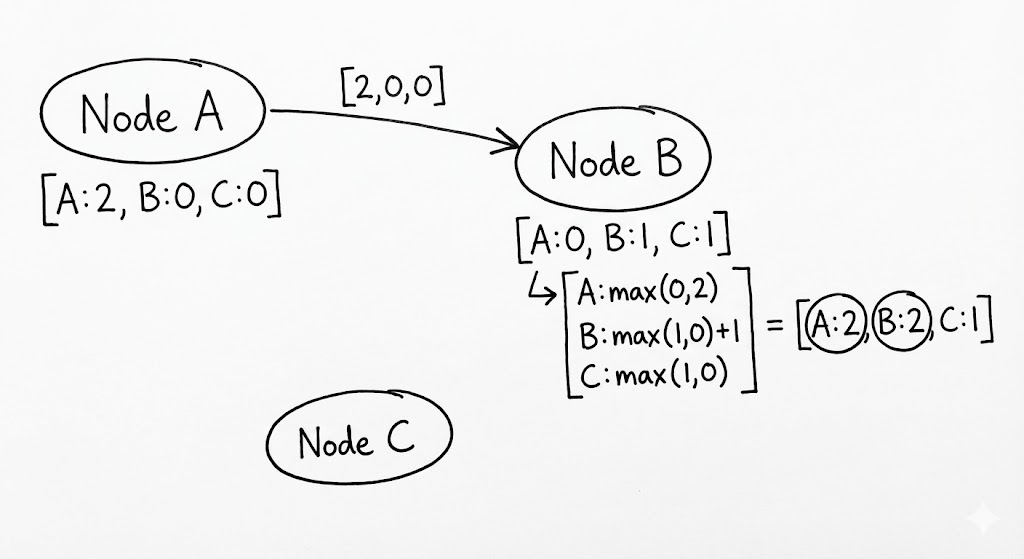
- 메시지 수신: 프로세스 $P_i$가 메시지와 함께 벡터 $V_{msg}$를 받으면:
- 자신의 인덱스를 증가시킵니다: $V_i[i] = V_i[i] + 1$.
- 자신의 벡터와 받은 벡터의 각 요소를 비교하여 큰 값으로 갱신합니다: 모든 $j$에 대해, $V_i[j] = \max(V_i[j], V_{msg}[j])$.
이 ‘병합(Merge)’ 과정이 바로 디지털 다중우주의 항해 일지를 대조하는 핵심 순간입니다. 서로 다른 함선이 만났을 때, 각자가 경험한 우주의 진척도 중 가장 최신의 정보를 취합하여 자신의 일지를 최신화하는 것과 같습니다.
수학적 판별: 인과적 선후와 동시성의 구분
벡터 클럭이 램포트 시계보다 우월한 이유는 두 벡터를 비교함으로써 두 사건의 관계를 명확히 정의할 수 있기 때문입니다. 두 사건 $a, b$의 벡터를 각각 $V(a), V(b)$라고 할 때 관계는 다음과 같이 결정됩니다.
- 인과적 선후 ($a \rightarrow b$): $V(a)$의 모든 요소가 $V(b)$의 해당 요소보다 작거나 같고, 적어도 하나의 요소는 엄격히 작을 때. ($V(a) \leq V(b) \land V(a) \neq V(b)$)
- 동시성 ($a \parallel b$): $V(a) < V(b)$도 아니고 $V(b) < V(a)$도 아닐 때. 즉, 어떤 요소는 $V(a)$가 크고 어떤 요소는 $V(b)$가 커서 서로 우위를 가릴 수 없는 상태입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import java.util.HashMap;
import java.util.Map;
import java.util.Set;
import java.util.HashSet;
/**
* 동시성(Concurrency) 감지 및 인과 관계 추적
*/
public class VectorClock {
private final String nodeId;
private final Map<String, Long> timestamps = new HashMap<>();
public enum Relation { BEFORE, AFTER, CONCURRENT, EQUAL }
public VectorClock(String nodeId) {
this.nodeId = nodeId;
this.timestamps.put(nodeId, 0L);
}
// 로컬 업데이트 및 병합 로직
public synchronized void tick() {
timestamps.put(nodeId, timestamps.getOrDefault(nodeId, 0L) + 1);
}
public synchronized void merge(Map<String, Long> other) {
tick();
other.forEach((id, time) ->
timestamps.put(id, Math.max(timestamps.getOrDefault(id, 0L), time))
);
}
/**
* 두 벡터 클럭의 관계를 비교하는 핵심 알고리즘
*/
public Relation compare(Map<String, Long> other) {
boolean smaller = false;
boolean larger = false;
Set<String> allKeys = new HashSet<>(timestamps.keySet());
allKeys.addAll(other.keySet());
for (String key : allKeys) {
long v1 = timestamps.getOrDefault(key, 0L);
long v2 = other.getOrDefault(key, 0L);
if (v1 < v2) smaller = true;
else if (v1 > v2) larger = true;
}
if (smaller && !larger) return Relation.BEFORE;
if (!smaller && larger) return Relation.AFTER;
if (smaller && larger) return Relation.CONCURRENT;
return Relation.EQUAL;
}
}
이 수학적 엄밀함 덕분에 분산 데이터베이스는 두 쓰기 작업이 ‘충돌’했는지(동시성), 아니면 하나가 다른 하나를 ‘덮어쓰기’ 했는지(인과성)를 완벽하게 판단할 수 있게 되었습니다.
Causal Consistency & Conflict Detection
이론적으로 완벽해 보이는 벡터 클럭이 실제 엔지니어링 현장에서 빛을 발하는 순간은 바로 ‘쓰기 충돌(Write Conflict)’을 해결할 때입니다. 분산 데이터베이스인 Amazon Dynamo나 Riak은 가용성을 극대화하기 위해 여러 노드에서 동시에 쓰기 작업을 허용하는데, 이때 각 노드의 항해 일지(벡터 클럭)를 대조하여 데이터의 운명을 결정합니다.
모든 노드가 즉각적으로 동일한 상태를 보여야 하는 선형성(Linearizability)은 강력하지만, 네트워크 파티션 상황에서 가용성을 포기해야 하는 대가가 따릅니다. 반면, 인과적 일관성(Causal Consistency)은 “원인이 결과보다 먼저 보여야 한다”는 최소한의 질서만을 약속합니다.
이 우주에서 A가 질문을 던지고 B가 답을 했다면, 이 답을 보는 모든 관찰자는 반드시 질문도 함께 보거나 혹은 질문을 먼저 보았음이 보장되어야 합니다. 질문 없는 답변이 존재하는 인과적 역설을 방지하는 도구가 바로 벡터 클럭입니다.
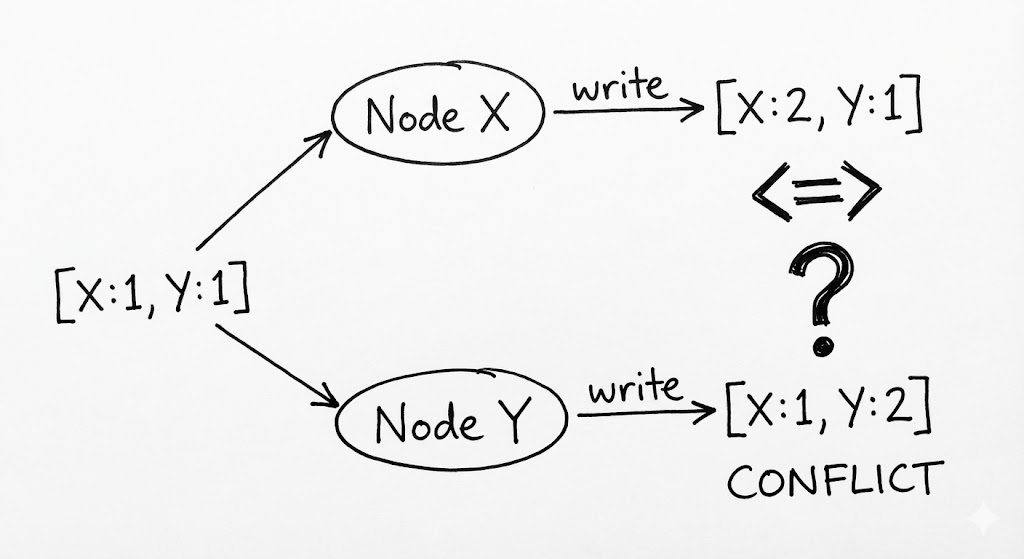
데이터베이스에 두 개의 서로 다른 값이 들어왔을 때, 시스템은 벡터 클럭을 비교합니다.
- 계승(Succession): 한 벡터가 다른 벡터보다 크다면, 이는 단순히 최신화된 상태입니다. 이전 데이터는 안전하게 버려집니다.
- 분기(Divergence): 두 벡터의 우위를 가릴 수 없다면(Concurrent), 시스템은 이를 ‘충돌’로 규정합니다.
이 충돌 상황에서 시스템은 독단적으로 결정을 내리지 않습니다. 대신, 두 버전을 모두 저장한 뒤 읽기 요청이 들어왔을 때 클라이언트에게 “우주가 두 갈래로 나뉘었는데, 어떤 것이 진짜인가요?”라고 되묻습니다. 이것이 바로 Riak에서 말하는 ‘형제(Siblings)’ 데이터의 정체입니다.
앞서 언급한 ‘항해 일지’ 비유를 다시 떠올려 봅시다. 두 함선이 우주 기지에서 만났을 때 각자의 일지를 펼칩니다.
- 함선 A의 일지: [지구 출발, 화성 통과, 목성 도착]
- 함선 B의 일지: [지구 출발, 화성 통과]
기지는 함선 A의 기록이 B를 포함하면서 더 진전되었음을 즉시 알 수 있습니다. 하지만 만약 함선 B의 기록이 [지구 출발, 금성 통과]라면 어떨까요? 두 함선은 화성과 금성이라는 서로 다른 경로를 택했고, 기지는 이 두 우주를 하나로 합치기 위해 엔지니어(클라이언트)의 개입을 요청하게 됩니다.
Last Write Wins (LWW)의 위험성
많은 시스템이 복잡한 벡터 클럭 대신 ‘가장 최근의 타임스탬프가 이긴다’는 LWW 방식을 택합니다. 하지만 이는 물리적 시계의 오차에 운명을 맡기는 위험한 도박입니다. 수 밀리초 차이로 발생한 중요한 결제 기록이 단지 서버 시계가 조금 느리다는 이유로 증발할 수 있기 때문입니다. 인과 관계를 추적한다는 것은 데이터의 소실을 방지하는 가장 강력한 방어선입니다.
Scalability Trade-offs
벡터 클럭은 분산 시스템의 인과 관계를 추적하는 가장 정교한 도구이지만, 공짜는 아닙니다. 엔지니어링의 세계에서 ‘완벽한 정합성’은 언제나 ‘확장성’이라는 비용과 맞교환됩니다. 시스템의 규모가 커질수록 벡터 클럭이 가졌던 우아함은 복잡성과 성능 저하라는 무거운 짐으로 변질되기 시작합니다.
식별자 팽창과 프루닝
벡터 클럭의 가장 근본적인 한계는 배열의 크기가 시스템 내의 노드 수($N$)에 정비례한다는 점입니다. 수십 대의 서버로 구성된 클러스터에서는 큰 문제가 되지 않지만, 수천 개의 마이크로서비스나 수만 명의 클라이언트가 직접 데이터를 수정하는 환경에서는 상황이 달라집니다. 모든 데이터 객체마다 수 킬로바이트의 벡터를 매달고 다니는 것은 네트워크 대역폭과 저장 공간 측면에서 엄청난 낭비입니다.
특히 모바일 기기처럼 접속과 해제가 빈번한 ‘동적 노드’ 환경에서는 문제가 더욱 심각해집니다. 각 클라이언트에게 벡터의 인덱스를 할당하다 보면, 이미 시스템을 떠난 사용자의 흔적이 벡터 클럭에 영원히 남아 배열이 무한히 비대해지는 ‘식별자 팽창(Identifier Explosion)’ 현상이 발생합니다.
이 문제를 해결하기 위해 Riak과 같은 시스템은 ‘프루닝(Pruning)’이라 불리는 기법을 사용합니다. 일정 크기 이상으로 커진 벡터 클럭에서 가장 오래된 항목을 강제로 삭제하는 일종의 가비지 컬렉션입니다. 하지만 이는 위험한 도박입니다.
프루닝의 트레이드오프
벡터의 일부를 삭제하는 순간, 벡터 클럭이 보장하던 ‘인과 관계의 완벽한 추적’은 깨집니다. 삭제된 정보를 기반으로 인과 관계를 판단하려 할 때, 시스템은 실제로 인과 관계가 있음에도 불구하고 이를 ‘충돌(Concurrent)’로 잘못 판단하는 허위 양성(False Positive) 오류를 범하게 됩니다. 결국 시스템은 데이터 유실을 막기 위해 불필요한 충돌 해결 과정을 거치게 되며, 이는 전체적인 성능 저하로 이어집니다.
Dotted Version Vectors
최근의 분산 시스템 아키텍처는 벡터 클럭의 한계를 극복하기 위해 Dotted Version Vectors(DVV) 같은 더 진보된 메커니즘을 도입합니다. DVV는 서버 수에 의존하는 기존 방식과 달리, 각 데이터 수정 이벤트에 고유한 ‘점(Dot)’을 부여하고 이를 버전 벡터와 결합합니다. 이를 통해 서버의 개수가 늘어나더라도 벡터의 크기를 효율적으로 제어하면서, 동시에 인과 관계가 없는 ‘형제(Siblings)’ 데이터들을 정확하게 구별해낼 수 있습니다.
결국 분산 시스템을 설계한다는 것은 어떤 수준의 불확실성을 감내할 것인지를 결정하는 과정입니다. 완벽한 인과성이 필요한 금융 결제 시스템이라면 벡터 클럭의 비용을 기꺼이 지불해야 할 것이며, 단순히 소셜 미디어의 ‘좋아요’ 숫자를 맞추는 정도라면 훨씬 가벼운 LWW(Last Write Wins) 방식이 정답일 수 있습니다. 우리는 기술의 화려함이 아니라, 비즈니스가 요구하는 정합성의 밀도에 따라 도구를 선택해야 합니다.
Summary
분산 시스템에서 시간은 물리적 수치가 아닌 ‘사건의 순서’라는 추상적 개념으로 재정의되어야 합니다. 물리적 시계의 불완전성을 극복하기 위해 등장한 램포트 시계는 인과 관계를 보존하는 부분 순서의 토대를 마련했으며, 이어 등장한 벡터 클럭은 다차원적 상태 기록을 통해 인과 관계의 역추적과 동시성 판별을 가능케 했습니다. 이러한 논리적 시간의 메커니즘은 현대 분산 데이터베이스가 데이터 충돌을 감지하고 인과적 일관성을 유지하는 핵심 장치로 작동합니다.