[Data Structure] Hash
컴퓨터 과학의 역사는 거대한 데이터 더미 속에서 원하는 정보를 얼마나 빨리 찾아낼 수 있느냐는 질문에 대한 답을 찾아가는 과정이었습니다. 데이터가 적을 때는 순차적으로 훑는 것만으로도 충분했으나, 데이터가 기하급수적으로 늘어남에 따라 우리는 선형적인 탐색 시간을 허용할 수 없게 되었습니다. 정렬된 데이터를 전제로 한 이진 탐색조차 $O(\log n)$이라는 비용을 요구합니다. 하지만 우리는 $O(1)$, 즉 데이터의 크기와 상관없이 즉각적으로 정보에 도달하는 마법 같은 성능을 갈망해 왔습니다.
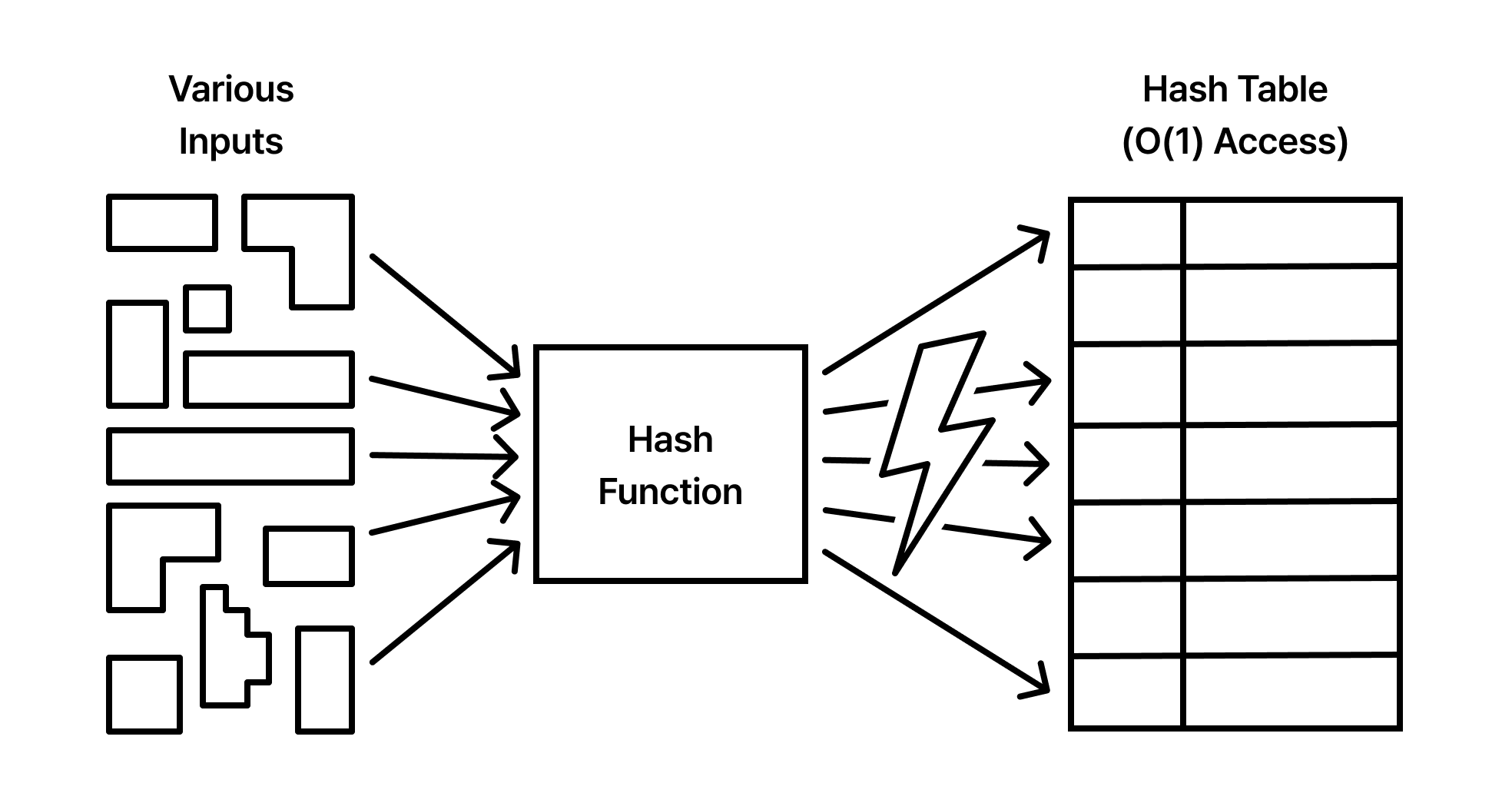
이 갈망을 현실로 만든 기술이 바로 해시(Hash)입니다. 해시는 복잡하고 무질서한 입력값을 정제된 고정 길이의 숫자로 변환하여, 데이터가 저장될 위치를 즉석에서 계산해 냅니다. 이는 마치 수만 권의 책이 꽂힌 도서관에서 책 제목만 보고도 몇 번째 복도, 몇 번째 선발에 그 책이 있는지 단번에 맞히는 사서와 같습니다. 오늘날 해시는 단순한 자료구조를 넘어 데이터베이스 인덱싱, 암호화, 분산 시스템의 데이터 배분 등 현대 컴퓨팅의 모든 계층에 스며들어 성능의 임계점을 돌파하는 핵심 엔진으로 작동하고 있습니다.
🧩 Hash Function
해시 함수는 임의의 길이를 가진 데이터를 입력받아 고정된 길이의 비트열(해시 값)로 출력하는 결정론적 알고리즘입니다. 이는 해시 테이블의 성능을 결정짓는 가장 핵심적인 하드웨어이자 소프트웨어적 설계 요소입니다. 좋은 해시 함수는 단순히 값을 변환하는 것을 넘어, 입력값의 미세한 변화에도 출력값이 완전히 달라지는 눈사태 효과(Avalanche Effect)를 동반하며 결과값을 전체 공간에 고르게 분산시켜야 합니다.
Determinism and Uniformity
해시 함수의 첫 번째 원칙은 결정론(Determinism)입니다. 동일한 입력값 $x$에 대해 해시 함수 $H(x)$는 언제나 동일한 출력값 $y$를 보장해야 합니다. 만약 이 일관성이 깨진다면, 데이터를 저장할 때 계산한 위치와 찾을 때 계산한 위치가 달라져 데이터 구조로서의 기능을 상실하게 됩니다.
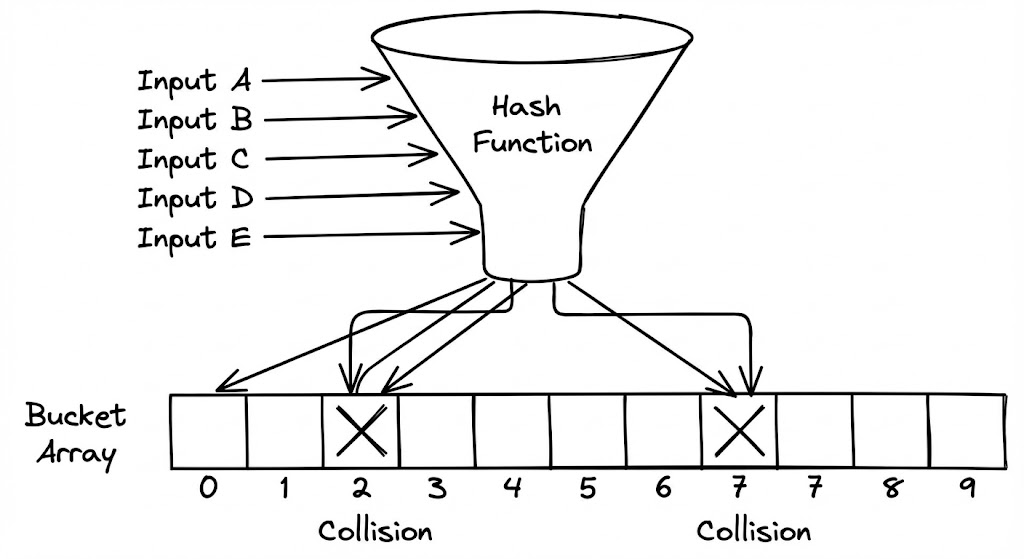
두 번째는 균일성(Uniformity)입니다. 입력 데이터의 분포가 편향되어 있더라도, 출력되는 해시 값은 전체 출력 범위(Hash Range) 내에 확률적으로 고르게 퍼져야 합니다. 특정 영역으로 해시 값이 몰리는 현상은 뒤에서 다룰 ‘충돌(Collision)’의 빈도를 높이며, 이는 해시 테이블의 탐색 성능을 $O(1)$에서 $O(n)$으로 급격히 퇴화시키는 주범이 됩니다.
The Modulo and Beyond
가장 원시적이면서도 강력한 해시 방법은 제법(Division Method)입니다. 입력값 $k$를 해시 테이블의 크기 $m$으로 나눈 나머지를 인덱스로 사용하는 방식입니다.
\[h(k) = k \mod m\]이 방식에서 $m$의 선택은 매우 치명적입니다. 만약 $m$이 2의 거듭제곱($2^p$)이라면, 해시 값은 입력값 $k$의 하위 비트들에만 의존하게 되어 패턴이 반복될 위험이 큽니다. 따라서 전통적으로 $m$은 2의 거듭제곱과 멀리 떨어진 소수(Prime Number)를 선택하는 것이 권장됩니다.
현대적 설계에서는 곱셈법(Multiplication Method)이나 Knuth의 곱셈 해싱 등을 사용하여 비트 연산의 효율성을 극대화합니다. 이는 실수 $A$($0 < A < 1$)를 곱한 뒤 소수점 아래 부분만을 취해 $m$을 곱하는 방식으로, 테이블 크기 $m$이 소수가 아니어도 비교적 양호한 분산도를 보여줍니다.
Cryptographic vs Non-cryptographic Hashing
엔지니어는 목적에 따라 해시 함수를 선택해야 합니다.
Non-cryptographic Hash (MurmurHash, CityHash, SipHash): 자료구조(Hash Table) 내에서 데이터를 빠르게 배치하는 것이 주된 목적입니다. 보안성보다는 처리 속도(Throughput)와 낮은 충돌율에 최적화되어 있습니다. 특히
SipHash는 해시 플러딩(Hash Flooding) 공격, 즉 의도적으로 충돌을 일으켜 서버 가용성을 떨어뜨리는 공격을 방어하기 위해 설계되어 최신 언어(Rust, Python 등)의 기본 해시 알고리즘으로 채택되었습니다.Cryptographic Hash (SHA-256, BLAKE3): 데이터의 무결성 검증과 보안이 목적입니다. ‘역상 저항성(Pre-image Resistance)’과 ‘충돌 저항성(Collision Resistance)’을 보장해야 하므로 연산 복잡도가 매우 높습니다. 단순히 자료구조의 인덱스를 계산하기 위해 SHA-256을 사용하는 것은 CPU 자원을 낭비하는 비효율적인 설계입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class HashComparison {
/**
* 1. Simple Polynomial Hash (Java의 String.hashCode 기본 원리)
* s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
*/
public static int simpleHash(String key, int bucketSize) {
int h = 0;
// 31은 소수이면서 비트 연산(h << 5 - h)으로 최적화가 가능하여 자주 사용됩니다.
for (int i = 0; i < key.length(); i++) {
h = 31 * h + key.charAt(i);
}
// 음수 결과 방지를 위해 비트 마스킹 후 나머지 연산
return (h & 0x7fffffff) % bucketSize;
}
public static void main(String[] args) {
String[] keys = {"apple", "apply", "applet", "banana", "cherry"};
int bucketSize = 1024;
System.out.printf("%-10s | %-15s | %-15s\n", "Key", "Simple Hash", "Java hashCode()");
System.out.println("-".repeat(50));
for (String k : keys) {
int sHash = simpleHash(k, bucketSize);
// Java 내장 hashCode() 사용
int jHash = (k.hashCode() & 0x7fffffff) % bucketSize;
System.out.printf("%-10s | %-15d | %-15d\n", k, sHash, jHash);
}
}
}
Java의 String 클래스는 hashCode를 한 번 계산하면 내부에 캐싱하여 재사용합니다. 반면, MurmurHash와 같은 현대적 알고리즘은 CPU의 SIMD 명령어를 활용하여 대량의 데이터를 바이트 단위가 아닌 블록 단위로 처리하여 압도적인 속도를 보여줍니다.
해시 함수의 성능 트레이드오프
해시 함수가 복잡해질수록 충돌은 줄어들지만, 인덱스를 계산하는 데 소요되는 CPU 사이클은 늘어납니다. 반대로 너무 간단한 함수는 계산은 빠르지만 충돌로 인한 추가 탐색 비용을 발생시킵니다. 따라서 현대의 고성능 시스템은 데이터의 특성과 하드웨어의 SIMD 지원 여부를 고려하여 최적의 함수를 선택합니다.
🧩 Hash Table
해시 함수가 추상적인 ‘계산 규칙’이라면, 해시 테이블은 그 규칙이 실체화되는 ‘물리적 공간’입니다. 해시 테이블의 본질은 공간을 미리 할당해 두고, 키를 인덱스로 변환하여 데이터에 즉시 접근하는 방식에 있습니다. 이는 시간 복잡도를 공간 복잡도로 치환하는 전형적인 트레이드오프의 산물입니다.
Direct Address Table의 한계와 추상화
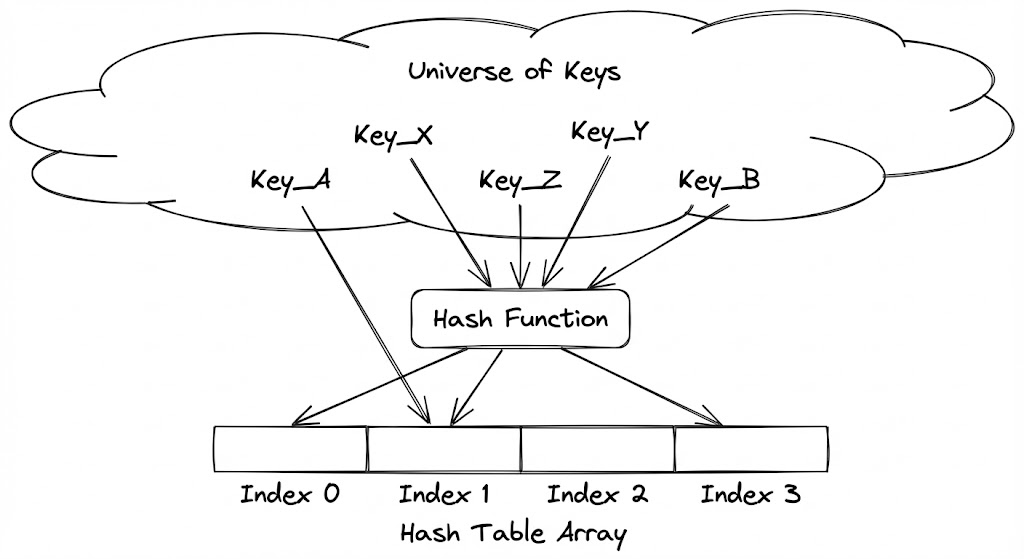
해시 테이블의 조상은 직접 주소 테이블(Direct Address Table)입니다. 키 집합 $U$가 작을 때, 각 키 $k$를 배열의 인덱스 $k$에 직접 매핑하는 방식입니다. 이 방식은 완벽한 $O(1)$을 보장하지만, 키의 범위가 커지면 치명적인 결함을 드러냅니다. 예를 들어, 10자리 학번을 인덱스로 쓰려면 100억 개의 슬롯을 가진 배열이 필요합니다. 실제 학생 수가 1,000명뿐이라도 말입니다.
해시 테이블은 이 광활한 키 공간을 실제 저장할 데이터 개수에 비례하는 작은 공간 $m$으로 압축(Hashing)함으로써 메모리 효율성을 확보합니다. 즉, 해시 테이블은 ‘가능한 모든 키’가 아닌 ‘실제 사용되는 키’를 위한 슬롯을 관리하는 추상화된 배열입니다.
Key-to-Index Mapping Mechanism
해시 함수가 생성한 결과값은 대개 매우 큰 정수입니다. 이를 실제 배열의 인덱스로 바꾸기 위해서는 테이블의 크기 $m$에 맞게 조정하는 과정이 필요합니다. 가장 보편적인 방식은 앞서 언급한 나머지 연산($hash(key) \mod m$)입니다.
하지만 현대적인 고성능 해시 테이블은 단순히 나머지를 구하는 데 그치지 않습니다. $m$을 2의 거듭제곱으로 유지하면서 비트 마스킹(hash & (m-1)) 연산을 사용하여 CPU 사이클을 아낍니다. 또한, 해시 함수의 결과값 상위 비트들이 인덱스 결정에 골고루 반영되도록 비트 믹싱(Bit Mixing) 과정을 추가하여, 비슷한 키들이 특정 인덱스에 몰리는 현상을 방지합니다.
메모리 레이아웃과 데이터 정렬
해시 테이블의 성능은 단순 연산 횟수보다 메모리 계층 구조(Memory Hierarchy)와의 친화력에서 결정됩니다. 데이터가 메모리상에 연속적으로 배치되어 있는지, 아니면 포인터를 통해 여기저기 흩어져 있는지는 CPU 캐시 히트율에 막대한 영향을 미칩니다.
전통적인 해시 테이블은 키와 값을 하나의 구조체로 묶어 배열에 저장하지만, 현대적인 설계(예: Google의 Swiss Tables)는 키의 일부 비트(H1)는 인덱스 결정에, 나머지 비트(H2)는 별도의 메타데이터 제어 바이트(Control Byte) 배열에 저장합니다. CPU는 실제 데이터를 뒤지기 전에 이 작은 메타데이터 배열을 먼저 스캔하여 후보군을 압축하며, 이때 SIMD 명령어를 사용하여 한 번에 16개 이상의 슬롯을 동시에 확인하는 극단적인 최적화를 수행합니다.
🧩 Collision
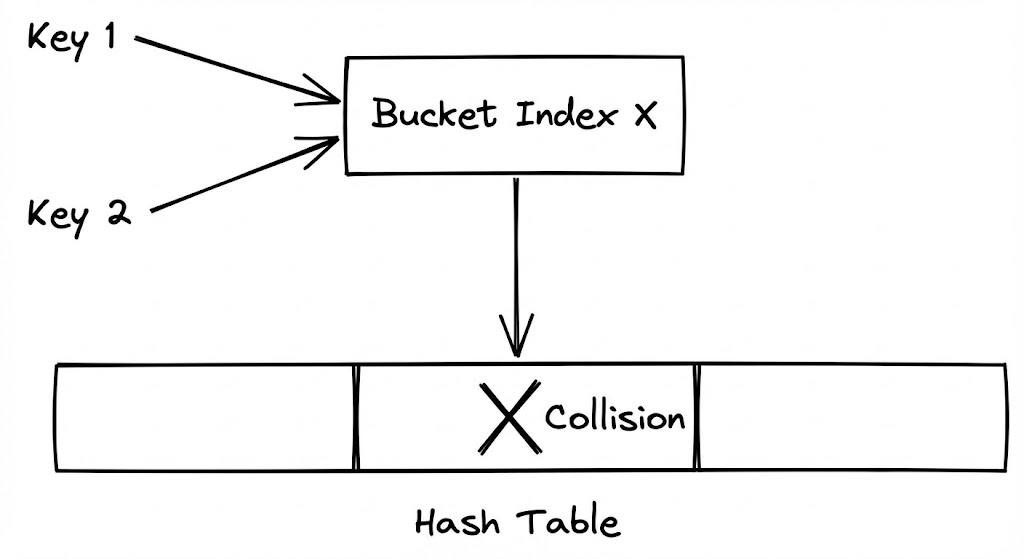
해시 테이블의 세계에서 충돌(Collision)은 예외 상황이 아니라 ‘상수’입니다. 서로 다른 두 키 $k_1, k_2$에 대해 $h(k_1) = h(k_2)$가 성립하는 순간, 우리는 이 충돌을 어떻게 우아하게 처리할지 결정해야 합니다.
비둘기집 원리와 확률적 필연성
수학적으로 충돌은 피할 수 없습니다. 비둘기집 원리(Pigeonhole Principle)에 따르면, $n$개의 아이템을 $m$개의 구멍에 넣을 때 $n > m$이면 최소한 한 구멍에는 두 개 이상의 아이템이 들어갑니다. 하지만 해시 테이블에서는 $n < m$인 상황에서도 충돌이 빈번하게 발생합니다. 이는 우리가 다루는 데이터가 무작위적이지 않거나, 해시 함수의 분산 능력이 완벽하지 않기 때문만은 아닙니다.
Birthday Paradox
생일 역설(Birthday Paradox)은 해시 충돌의 확률적 공포를 잘 보여줍니다. 23명만 모여도 그중 생일이 같은 사람이 있을 확률은 50%가 넘습니다. 365라는 넓은 범위(테이블 크기)에 비해 23명(데이터 개수)은 매우 적음에도 불구하고 충돌은 예상보다 훨씬 빨리 일어납니다.
해시 테이블에서도 마찬가지입니다. 테이블이 절반도 차지 않았음에도 불구하고 특정 슬롯에서 충돌이 발생할 확률은 기하급수적으로 상승합니다. 엔지니어는 “테이블이 꽉 차면 충돌이 나겠지”라고 낙관해서는 안 되며, 첫 번째 데이터를 넣는 순간부터 충돌 대응 전략을 가동해야 합니다.
충돌 밀도에 따른 성능 저하 곡선
충돌이 발생하면 $O(1)$의 성능은 무너지기 시작합니다. 충돌된 데이터를 찾기 위해 추가적인 탐색(Probing)이나 리스트 순회(Traversing)가 발생하기 때문입니다.
중요한 점은 성능 저하가 선형적으로 일어나지 않는다는 것입니다. 특정 임계점(보통 부하율 70~80%)을 넘어서는 순간, 충돌이 충돌을 낳는 연쇄 반응(Clustering)이 일어나며 성능은 절벽 아래로 떨어집니다. 따라서 해시 테이블 설계의 핵심은 이 ‘성능 절벽’이 나타나기 전에 공간을 재배치하거나, 충돌의 파급력을 최소화하는 알고리즘을 선택하는 데 있습니다.
충돌은 결함이 아닌 설계의 일부
완벽하게 충돌이 없는 ‘퍼펙트 해싱(Perfect Hashing)’은 정적인 데이터셋에서만 가능합니다. 동적인 환경에서는 충돌을 막는 데 자원을 쓰기보다, 충돌이 발생했을 때 얼마나 빠르게 다음 후보지를 찾느냐(Collision Resolution)에 집중하는 것이 훨씬 경제적인 엔지니어링입니다.
🧩 Bucket & Slot
해시 테이블의 내부를 들여다보면, 데이터가 단순히 ‘담기는’ 것이 아니라 엄격한 레이아웃에 따라 ‘배치’됨을 알 수 있습니다. 이때 최소 단위가 되는 공간이 버킷(Bucket)과 슬롯(Slot)입니다.
데이터의 물리적 안착 지점
버킷은 해시 함수에 의해 직접적으로 지칭되는 주소 공간입니다. 하나의 버킷은 하나 이상의 슬롯을 포함할 수 있습니다. 가장 단순한 형태의 해시 테이블에서는 ‘1 버킷 = 1 슬롯’의 구조를 가지지만, 하드웨어 최적화가 적용된 현대적 아키텍처에서는 하나의 버킷이 CPU 캐시 라인 크기(주로 64바이트)에 맞춰 설계되어 여러 개의 슬롯을 한꺼번에 담기도 합니다.
이러한 설계의 목적은 공간 지역성(Spatial Locality)입니다. 해시 충돌이 발생하여 인접한 슬롯을 검사해야 할 때, 이미 같은 버킷(캐시 라인)에 데이터가 로드되어 있다면 추가적인 메인 메모리 접근 없이 L1/L2 캐시 수준에서 탐색을 끝낼 수 있기 때문입니다.
슬롯의 구조와 메타데이터 관리
슬롯은 단순히 값(Value)만 저장하는 장소가 아닙니다. 일반적인 슬롯은 (Key, Value, State)의 튜플 구조를 가집니다. 여기서 State는 해당 슬롯이 비어 있는지(Empty), 데이터가 차 있는지(Occupied), 혹은 데이터가 있었다가 삭제되었는지(Deleted/Tombstone)를 나타내는 메타데이터입니다.
특히 ‘Deleted’ 상태의 관리는 Open Addressing 방식에서 매우 중요합니다. 삭제된 슬롯을 단순히 ‘Empty’로 표시하면, 충돌로 인해 뒤쪽에 저장된 데이터를 찾는 탐색 경로가 끊어지기 때문입니다. 이를 방지하기 위해 ‘비어있지만 이전 탐색의 연결 고리 역할을 하는’ 묘비(Tombstone) 데이터가 필요하며, 이는 슬롯의 복잡성을 높이는 요인이 됩니다.
🧩 Load Factor
해시 테이블의 효율성은 ‘얼마나 많은 공간이 비어있는가’에 의존합니다. 이를 정량화한 지표가 부하율(Load Factor, $\alpha$)입니다.
\[\alpha = \frac{n}{m}\]여기서 $n$은 저장된 키의 개수, $m$은 전체 슬롯의 개수입니다.
밀도와 탐색 성능의 상관관계
부하율은 탐색 성능과 반비례 관계에 있습니다. $\alpha$가 0에 가까우면 충돌 확률이 낮아 $O(1)$에 수렴하지만, 메모리 낭비가 심해집니다. 반대로 $\alpha$가 1에 가까워지면 충돌이 빈번해져 탐색 시간은 선형적으로, 혹은 지수적으로 증가합니다.
컴퓨터 과학의 수많은 실험적 결과에 따르면, 대부분의 해시 테이블 구현체는 $\alpha \approx 0.7$ 내외에서 리사이징을 결정합니다. 이는 메모리 효율성과 탐색 속도 사이의 황금비(Golden Ratio)로 여겨지며, 이 임계점을 넘어서는 순간 ‘성능의 퇴화’가 공학적으로 감당하기 어려운 수준이 됩니다.
Collision Resolution at Scale
충돌을 해결하는 두 가지 거대한 패러다임은 데이터 구조의 운명을 결정합니다.
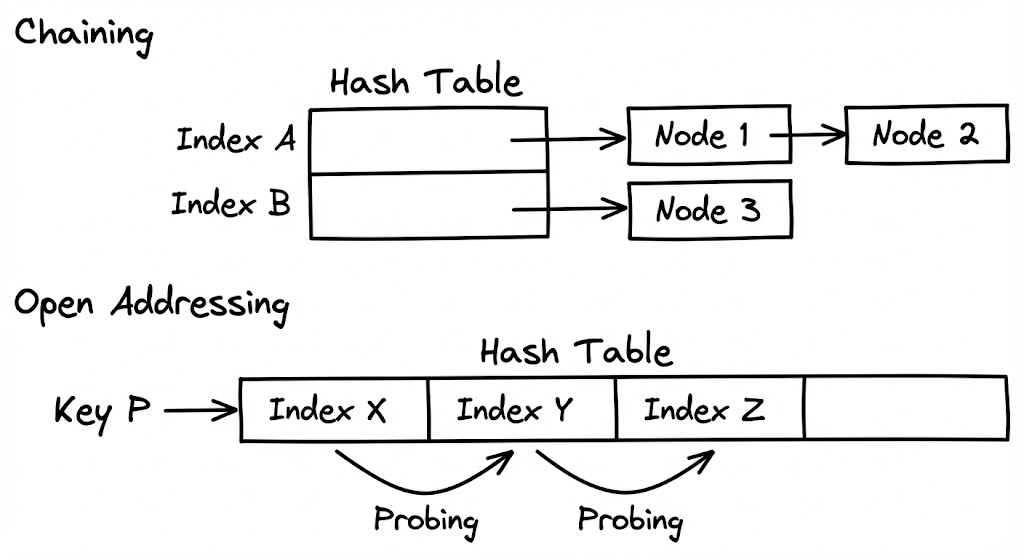
Separate Chaining의 메모리 오버헤드
Separate Chaining은 각 버킷을 연결 리스트(Linked List)의 헤드로 만드는 방식입니다. 충돌이 발생하면 해당 버킷의 리스트 끝에 새 데이터를 매달기만 하면 되므로 구현이 간단하고, 부하율이 1을 넘어가도(슬롯보다 데이터가 많아져도) 작동한다는 장점이 있습니다.
하지만 치명적인 단점은 메모리 파편화입니다. 리스트의 노드들이 메모리 곳곳에 흩어져 저장되므로, 탐색 시 포인터를 따라갈 때마다 CPU 캐시 미스가 발생합니다. 이는 이론적인 시간 복잡도가 $O(1 + \alpha)$임에도 불구하고, 실제 하드웨어에서는 Open Addressing보다 훨씬 느리게 작동하는 원인이 됩니다.
Open Addressing과 캐시 지역성
Open Addressing은 모든 데이터를 배열 자체(내부 공간)에 담습니다. 충돌이 나면 정해진 규칙(Probing)에 따라 다음 비어있는 슬롯을 찾아 나섭니다.
- Linear Probing: $h(k, i) = (h’(k) + i) \mod m$. 바로 옆 칸을 확인합니다. 캐시 효율은 최강이지만, 데이터가 뭉치는 클러스터링(Clustering) 현상에 매우 취약합니다.
- Quadratic Probing: $i$의 제곱수만큼 건너뛰며 탐색합니다. 클러스터링을 완화하지만 여전히 완벽하지 않습니다.
- Double Hashing: 두 번째 해시 함수를 사용하여 건너뛸 간격을 결정합니다. 클러스터링을 가장 효과적으로 방지합니다.
Clustering Problem
선형 조사법에서 발생하는 일차 클러스터링(Primary Clustering)은 해시 테이블의 재앙입니다. 한 번 데이터가 뭉치기 시작하면, 그 뭉치에 걸리는 모든 해시 값은 뭉치의 끝까지 탐색을 강요당하고, 결과적으로 뭉치의 크기를 더 키우는 악순환에 빠집니다. 이는 특정 구간의 밀도가 급격히 높아져 전체적인 평균 탐색 시간을 오염시킵니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import java.util.Arrays;
public class LinearProbingHashTable<K, V> {
// 삭제된 슬롯을 표시하기 위한 공유 객체 (Tombstone)
private static final Object TOMBSTONE = new Object();
private int capacity;
private K[] keys;
private V[] values;
@SuppressWarnings("unchecked")
public LinearProbingHashTable(int capacity) {
this.capacity = capacity;
this.keys = (K[]) new Object[capacity];
this.values = (V[]) new Object[capacity];
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % capacity;
}
public void put(K key, V value) {
int i = hash(key);
// 슬롯이 비어있지 않고, Tombstone도 아니며, 키가 다를 경우 다음 칸으로 이동
while (keys[i] != null && keys[i] != TOMBSTONE) {
if (keys[i].equals(key)) {
values[i] = value; // 업데이트
return;
}
i = (i + 1) % capacity;
}
keys[i] = key;
values[i] = value;
}
public V get(K key) {
int i = hash(key);
while (keys[i] != null) {
// Tombstone은 무시하고(Skip) 탐색을 계속 진행해야 함
if (keys[i] != TOMBSTONE && keys[i].equals(key)) {
return values[i];
}
i = (i + 1) % capacity;
}
return null; // 탐색 실패
}
public void delete(K key) {
int i = hash(key);
while (keys[i] != null) {
if (keys[i] != TOMBSTONE && keys[i].equals(key)) {
// 물리적으로 삭제하는 대신 Tombstone으로 교체
keys[i] = (K) TOMBSTONE;
values[i] = null;
return;
}
i = (i + 1) % capacity;
}
}
}
Java에서 위와 같은 방식은 객체 배열을 사용하므로 실제 데이터는 힙(Heap)에 흩어집니다. 최고의 성능을 위해서는 기본 타입 배열(Primitive Array)을 사용하여 캐시 라인 적중률을 높이는 설계(예: fastutil 라이브러리)가 권장됩니다.
Chaining과 Open Addressing의 선택 기준
데이터의 크기가 작고 삭제 연산이 빈번하다면 관리의 편의성을 위해 Chaining이 유리할 수 있습니다. 하지만 현대의 고성능 서버 환경에서 수억 개의 데이터를 다룬다면, 캐시 효율성을 극대화할 수 있는 Open Addressing(특히 Robin Hood Hashing이나 Swiss Tables 방식)을 선택하는 것이 압도적인 처리량을 보장합니다.
Dynamic Resizing and Amortized Analysis
해시 테이블은 고정된 크기의 배열에서 시작하지만, 데이터는 멈추지 않고 유입됩니다. 부하율($\alpha$)이 임계점에 도달하면, 시스템은 성능 고착을 막기 위해 더 큰 공간으로 이사해야 합니다. 이 과정을 리사이징(Resizing) 혹은 재해싱(Rehashing)이라 부릅니다.
Rehashing
단순히 배열의 크기를 키우는 것만으로는 부족합니다. 해시 테이블의 인덱스는 hash(key) % table_size에 의존하기 때문에, table_size가 변하는 순간 기존 데이터들의 인덱스는 모두 무효화됩니다. 따라서 리사이징은 단순히 새 공간을 할당하는 작업을 넘어, 기존의 모든 데이터를 하나하나 다시 꺼내어 새 해시 함수(혹은 새 크기)에 맞춰 재배치하는 $O(n)$의 과정을 수반합니다.
이 과정은 엔지니어링 관점에서 매우 위험한 순간입니다. 데이터가 수백만 개라면 리사이징이 일어나는 동안 시스템은 일시적으로 응답을 멈추는 ‘Stop-the-world’ 현상을 겪게 됩니다.
Amortized Analysis
그럼에도 불구하고 우리는 해시 테이블의 삽입 성능을 $O(1)$이라고 부릅니다. 이는 분할 상환 분석(Amortized Analysis) 덕분입니다. $n$번의 삽입 중 한 번의 삽입이 $O(n)$의 리사이징 비용을 발생시키더라도, 이를 앞선 $n-1$번의 $O(1)$ 작업들에 비용을 골고루 나누어(Amortize) 할당하면 평균적인 비용은 여전히 상수에 수렴한다는 논리입니다.
수학적으로, 배열의 크기를 2배씩 늘릴 때마다 각 원소는 리사이징 과정에서 최대 3번의 이동(자신의 삽입, 첫 번째 이사, 두 번째 이사…)만 겪으면 됩니다. 이 ‘잠재적 비용’의 합이 일정하기 때문에, 해시 테이블은 거대한 스케일에서도 이론적인 성능 우위를 유지할 수 있습니다.
Incremental Hashing을 통한 레이턴시 스파이크 방지
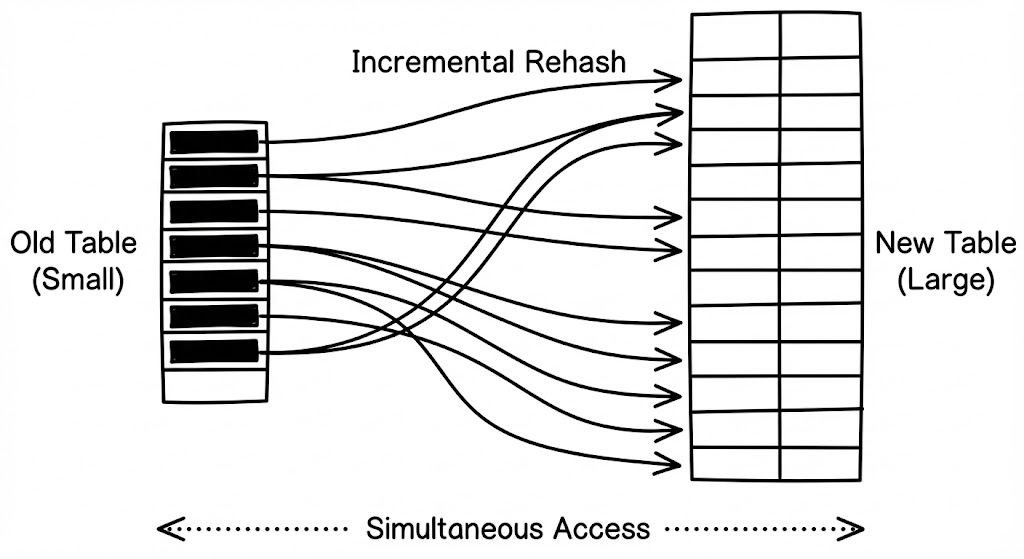
실시간성(Real-time)이 중요한 시스템에서는 한 번의 $O(n)$ 작업조차 허용되지 않습니다. 이를 위해 고안된 기법이 점진적 해싱(Incremental Hashing)입니다.
이 방식은 리사이징이 필요할 때 한꺼번에 모든 데이터를 옮기지 않습니다. 대신, 기존 테이블과 새 테이블을 동시에 유지하면서 삽입/삭제가 발생할 때마다 조금씩(예: 한 번의 작업당 1~10개의 버킷) 데이터를 옮깁니다. 모든 데이터가 옮겨지면 비로소 구버전 테이블을 메모리에서 해제합니다. 이는 시스템의 레이턴시 스파이크를 억제하여 예측 가능한 성능을 보장하는 현대적 데이터베이스와 캐시 시스템(Redis 등)의 핵심 전략입니다.
공간의 유연성과 성능의 상관관계
리사이징은 해시 테이블이 가진 ‘고정된 공간’이라는 한계를 깨고 동적인 확장을 가능케 합니다. 하지만 빈번한 리사이징은 메모리 할당자와 GC에 막대한 부담을 줍니다. 따라서 초기 데이터 양을 예측할 수 있다면, 테이블 생성 시 충분한 초기 용량(Initial Capacity)을 설정하여 리사이징 횟수를 최소화하는 것이 숙련된 시니어 엔지니어의 미덕입니다.
Summary
해싱은 복잡한 세상을 단순한 인덱스로 치환하여 무한한 탐색 시간을 상수의 찰나로 바꾼 컴퓨터 과학의 정수입니다. 성능의 핵심은 단순히 빠른 해시 함수를 만드는 데 있는 것이 아니라, 충돌의 확률적 필연성을 인정하고 하드웨어의 캐시 지역성을 극대화하는 물리적 레이아웃을 설계하는 데 있습니다. 부하율 관리를 통한 적절한 리사이징 전략과 하드웨어 친화적인 충돌 해결 방식을 결합할 때, 우리는 비로소 대규모 시스템에서도 무너지지 않는 진정한 $O(1)$의 마법을 누릴 수 있습니다.